Graph Theory · Discrete Mathematics · GATE CSE

Let $A$ be the adjacency matrix of a simple undirected graph $G$. Suppose $A$ is its own inverse. Which one of the following statements is always TRUE...

The number of spanning trees in a complete graph of 4 vertices labelled A, B, C, and D is __________

Which of the following statements is/are TRUE for a group G?

Consider a simple undirected graph of 10 vertices. If the graph is disconnected, then the maximum number of edges it can have is __________.

In an undirected connected planar graph G, there are eight vertices and five faces. The number of edges in G is ______

Let G be an undirected complete graph on n vertices, where n > 2. Then, the number of different Hamiltonian cycles in G is equal to

Let $$G$$ be a finite group on $$84$$ elements. The size of a largest possible proper subgroup of $$G$$ is ________.

The chromatic number of the following graph is _______. ...

The minimum number of colours that is sufficient to vertex-colour any planar graph is _____________ .

let $$G$$ be a group with $$15$$ elements. Let $$L$$ be a subgroup of $$G$$. It is known that $$L \ne G$$ and that the size of $$L$$ is at least $$4$$...

Let $$G = \left( {V,E} \right)$$ be a directed graph where $$V$$ is the set of vertices and $$E$$ the set of edges. Then which one of the following gr...

The maximum number of edges in a bipartite graph on $$12$$ vertices is _________.

Consider an undirected random$$^ \circ $$ graph of eight vertices. The probability that there is an edge between a pair of vertices is 1/2. What is th...

Which of the following statements is/are TRUE for undirected graphs? P: Number of odd degree vertices is even. Q: Sum of degrees of all vertices...

Let G be a simple undirected planner graph on 10 vertices with 15 edges. If G is a connected graph, then the number of bounded faces in any embedding ...

$$K4$$ and $$Q3$$ are graphs with the following structures. Which one of the following statements is TRUE in relation to these graphs?...

Let $$G$$ $$\,\,\,\,\, = \,\,\,\left( {V,\,\,\,\,\,E} \right)$$ be a graph. Define $$\xi \left( G \right) = \sum\limits_d {{i_d} \times } {\mkern 1mu}...

What is the chromatic number of an $$n$$-vertex simple connected graph which does not contain any odd length cycle? Assume $$n \ge 2$$.

Which one of the following is TRUE for any simple connected undirected graph with more than $$2$$ vertices?

What is the size of the smallest MIS (Maximal Independent Set) of a chain of nine nodes?

What is the chromatic number of the following graph? ...

Let $$G$$ be the non-planar graph with minimum possible number of edges. Then $$G$$ has

Consider a weighted undirected graph with positive edge weights and let $$uv$$ be an edge in the graph. It is known that the shortest path from the so...

The height of a binary tree is the maximum number of edges in any root to leaf path. The maximum number of nodes in a binary tree of height $$h$$ is:...

The maximum number of binary trees that can be formed with three unlabeled nodes is:

If all the edge weights of an undirected graph are positive, then any subject of edges that connects all the vertices and has minimum total weight is ...

Consider a weighted complete graph $$G$$ on the vertex set $$\left\{ {{v_1},\,\,\,{v_2},....,\,\,\,{v_n}} \right\}$$ such that the weight of the edge ...

Let $$G$$ be the simple graph with 20 vertices and 100 edges. The size of the minimum vertex cover of $$G$$ is 8. Then, the size of the maximum indepe...

Let $$G$$ be a simple connected planar graph with 13 vertices and 19 edges. Then, the number of faces in the planar embedding of the graph is:

What is the maximum number of edges in an acyclic undirected graph with $$n$$ vertices?

Let $$G$$ be an arbitrary graph with $$n$$ nodes and $$k$$ components. If a vertex is removed from $$G$$, the number of components in the resultant gr...

Maximum number of edges in a n - node undirected graph without self loops is

The number of distinct simple graph with upto three nodes is

Which of the following is/are tautology?

A non-planar graph with minimum number of vertices has

The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. The chromatic number of the following graph ...

The chromatic number of a graph is the minimum number of colours used in a proper colouring of the graph. Let $G$ be any graph with $n$ vertices and c...

The number of edges present in the forest generated by the DFS traversal of an undirected graph G with 100 vertices is 40. The number of connected com...

Let G be a simple, finite, undirected graph with vertex set {$$v_1,...,v_n$$}. Let $$\Delta(G)$$ denote the maximum degree of G and let N = {1, 2, ......

Let $$U = \{ 1,2,3\} $$. Let 2$$^U$$ denote the powerset of U. Consider an undirected graph G whose vertex set is 2$$^U$$. For any $$A,B \in {2^U},(A,...

Consider a simple undirected unweighted graph with at least three vertices. If A is the adjacency matrix of the graph, then the number of 3-cycles in ...

Consider a simple undirected weighted graph G, all of whose edge weights are distinct. Which of the following statements about the minimum spanning tr...

The following simple undirected graph is referred to as the Peterson graph. Which of the following statements is/are TRUE?...

Which of the properties hold for the adjacency matrix A of a simple undirected unweighted graph having n vertices?

In a directed acyclic graph with a source vertex s, the quality-score of a directed path is defined to be the product of the weights of the edges on t...

An articulation point in a connected graph is a vertex such that removing the vertex and its incident edges disconnects the graph into two or more con...

Let G be a group order 6, and H be a subgroup of G such that 1 < |H| < 6. Which one of the following options is correct?

Let G = (V, E) be an undirected unweighted connected graph. The diameter of G is defined as: diam(G) = $$\displaystyle\max_{u, x\in V}$$ {t...

Graph G is obtained by adding vertex s to K3,4 and making s adjacent to every vertex of K3,4. The minimum number of colours required to edge-colour G ...

Let G be any connected, weighted, undirected graph.I. G has a unique minimum spanning tree, if no two edges of G have the same weight.II. G has a uniq...

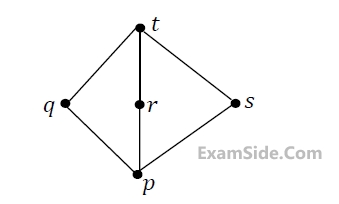Suppose L = { p, q, r, s, t } is a lattice represented by the following Hasse diagram: For any $$x, y ∈ L$$, not necessarily distinct, $$x ∨ y$$ and ...

Let G be a connected planar graph with 10 vertices. If the number of edges on each face is three, then the number of edges in G is ___________.

A graph is self-complementary if it is isomorphic to its complement. For all self-complementary graphs on $$n$$ vertices, $$n$$ is

In a connected graph, bridge is an edge whose removal disconnects a graph. Which one of the following statements is true?

A cycle on $$n$$ vertices is isomorphic to its complement. The value of $$n$$ is __________.

If $$G$$ is a forest with $$n$$ vertices and $$k$$ connected components, how many edges does $$G$$ have?

Let $$\delta $$ denote the minimum degree of a vertex in a graph. For all planar graphs on $$n$$ vertices with $$\delta \ge 3$$, which one of the fol...

Consider an undirectional graph $$G$$ where self-loops are not allowed. The vertex set of $$G$$ is $$\left\{ {\left( {i,j} \right):\,1 \le i \le 12,\,...

An ordered $$n$$-tuple $$\left( {{d_1},\,\,{d_2},\,....,{d_n}} \right)$$ with $${{d_1} \ge ,\,\,{d_2} \ge .... \ge {d_n}}$$ is called graphic if there...

The line graph $$L(G)$$ of a simple graph $$G$$ is defined as follows: $$\,\,\,\,$$There is exactly one vertex $$v(e)$$ in $$L$$(G)$$ for each edge $$...

Which of the following graphs is isomorphic to ...

Let $$G$$ be a complete undirected graph on $$6$$ vertices. If vertices of $$G$$ $$\,\,\,\,$$ are labeled, then the number of distinct cycles of lengt...

The degree sequence of a simple graph is the sequence of the degrees of the nodes in the graph in decreasing order. Which of the following sequences c...

A binary tree with $$n>1$$ nodes has $${n_1}$$, $${n_2}$$ and $${n_3}$$ nodes of degree one, two and three respectively. The degree of a node is de...

A binary tree with $$n>1$$ nodes has $${n_1}$$, $${n_2}$$ and $${n_3}$$ nodes of degree one, two and three respectively. The degree of a node is de...

$$G$$ is a graph on $$n$$ vertices and $$2n-2$$ edges. The edges of $$G$$ can be partitioned into two edge-disjoint spanning trees. Which of the follo...

$$G$$ is a simple undirected graph. Some vertices of $$G$$ are of odd degree. Add a node $$v$$ to $$G$$ and make it adjacent to each odd degree vertex...

Which of the following statements is true for every planar graph on $$n$$ vertices?

Let Graph$$(x)$$ be a predicate which denotes that $$x$$ is a graph. Let Connected$$(x)$$ be a predicate which denotes that $$x$$ is connected. Which ...

Which of the following graphs has an Eulerian circuit?

The $${2^n}$$ vertices of a graph $$G$$ correspond to all subsets of a set of size $$n$$, for $$n \ge 6$$. Two vertices of $$G$$ are adjacent if and o...

The $${2^n}$$ vertices of a graph $$G$$ correspond to all subsets of a set of size $$n$$, for $$n \ge 6$$. Two vertices of $$G$$ are adjacent if and o...

Consider the undirected graph $$G$$ defined as follows. The vertices of $$G$$ are bit strings of length $$n$$. We have an edge between vertex $$u$$ an...

Which one of the following graphs is NOT planar? ...

Let $${G_1} = \left( {V,\,{E_1}} \right)$$ and $${G_2} = \left( {V,\,{E_2}} \right)$$ be connected graphs on the same vertex set $$V$$ with more than ...

What is the number of vertices in an undirected connected graph with $$27$$ edges, $$6$$ vertices of degree $$2$$, $$\,\,$$ $$3$$ vertices of degree ...

How many graphs on $$n$$ labeled vertices exist which have at least $$\left( {{n^2} - 3n} \right)/2\,\,\,$$ edges?

The minimum number of colours required to colour the following graph, such that no two adjacent vertices are assigned the same colour, is ...

$$A$$ graph $$G$$ $$=$$ $$(V, E)$$ satisfies $$\left| E \right| \le \,3\left| V \right| - 6.$$ The min-degree of $$G$$ is defined as $$\mathop {\min ...

How many perfect matchings are there in a complete graph of 6 vertices?

how many undirected graphs (not necessarily connected) can be constructed out of a given $$\,\,\,\,V = \left\{ {{v_1},\,\,{v_2},\,....,\,\,{v_n}} \rig...

Prove that in a finite graph, the number of vertices of odd degree is always even.

Maximum number of edges in a planar graph with $$n$$ vertices is _______ .

The maximum number of possible edges in an undirected graph with a vertices and $$k$$ components is _________ .

A graph is planar if and only if,

Which of the following graphs is / are planar? (see fig.) ...

Let $$G$$ be a connected, undirected graph. A $$cut$$ in $$G$$ is a set of edges whose removal results in $$G$$ being broken into two or more componen...

How many minimum spanning tress does the following graph have? Draw them (Weights are assigned to the edges). ...