Finite Automata and Regular Language · Theory of Computation · GATE CSE
Marks 1
A regular language $L$ is accepted by a non-deterministic finite automaton (NFA) with $n$ states. Which of the following statement(s) is/are FALSE?
Which one of the following regular expressions is equivalent to the language accepted by the DFA given below?

Let $L_1, L_2$ be two regular languages and $L_3$ a language which is not regular. Which of the following statements is/are always TRUE?
Consider the Deterministic Finite-state Automation (DFA) $$A$$ shown below. The DFA runs on the alphabet {0, 1}, and has the set of states {$$s,p,q,r$$}, with $$s$$ being the start state and $$p$$ being the only final state.

Which one of the following regular expressions correctly describes the language accepted by $$A$$?
Consider the following definition of a lexical token id for an identifier in a programming language, using extended regular expressions:
$$\mathrm{letter\to[A-Za-z]}$$
$$\mathrm{letter\to[0-9]}$$
$$\mathrm{id\to letter(letter\,|\,digit)^*}$$
Which one of the following Non-deterministic Finite-state Automata with $$\varepsilon $$-transmissions accepts the set of valid identifiers? (A double-circle denotes a final state)
Which of the following statements is/are CORRECT?
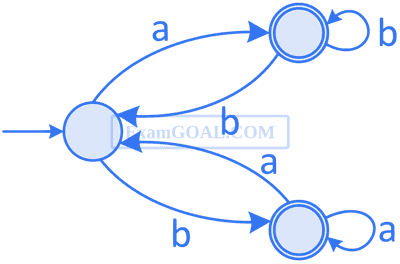
Which one of the following regular expressions correctly represents the language of the finite automation given below?
Consider the following deterministic finite automaton (DFA).

The number of strings of length 8 accepted by the above automaton is __________
I. If L1 $$ \cup $$ L2 is regular, then both L1 and L2 must be regular.
II. The class of regular languages is closed under infinite union.
Which of the above statements is/are TRUE?
is ___________________.
Language $${L_2}$$ is defined by the grammar: $$S{}_2 \to ab{S_2}|\varepsilon $$
Consider the following statements:
$$P:$$ $${L_1}$$ is regular
$$Q:$$ $${L_2}$$ is regular
Which one of the following is TRUE?

What is the set of reachable states for the input string $$0011?$$
$$\left. {\rm I} \right)$$ $$\,\,\,{L_{1 \bullet }}{L_2}$$ is a regular language
$$\left. {\rm II} \right)$$ $$\,\,\,{L_{1 \bullet }}{L_2} = \left\{ {{a^n}{b^n}\left| {n \ge \left. 0 \right\}} \right.} \right.$$
Which one of the following is CORRECT?
Assume $$\sum { = \left\{ a \right\}\,\,} $$ and $$\varepsilon $$ is the empty string.

$${S_1}\,\,:\,\,\left\{ {{0^{2n}}\left| {n \ge 1} \right.} \right\}$$ is a regular language
$${S_2}\,\,:\,\,\left\{ {{0^m}{1^n}{0^{m + n}}\left| {m \ge 1} \right.\,\,and\,\,n \ge \left. 1 \right\}} \right.$$ is a regular language
Which of the following statements is correct?
(i) $${\left( {00} \right)^ * }\left( {\varepsilon + 0} \right)$$
(ii) $${\left( {00} \right)^ * }$$
(iii) $${0^ * }$$
(iv) $$0\,\,{\left( {00} \right)^ * }$$
A FSM (Finite State Machine) can be designed to add two integers of any arbitrary length (arbitrary number of digits).
Marks 2
Let $\Sigma=\{a, b, c\}$. For $x \in \Sigma^{\star}$, and $\alpha \in \Sigma$, let $\#_\alpha(x)$ denote the number of occurrences of a in $x$. Which one or more of the following option(s) define(s) regular language(s)?
Let $\Sigma=\{1,2,3,4\}$ For $x \in \Sigma^*$, let prod $(x)$ be the product of symbols in $x$ modulo 7 . We take $\operatorname{prod}(\varepsilon)=1$, where $\varepsilon$ is the null string.
For example, $\operatorname{prod}(124)=(1 \times 2 \times 4) \bmod 7=1$.
Define $L=\left\{x \in \Sigma^{\star} \mid \operatorname{prod}(x)=2\right\}$.
The number of states in a minimum state DFA for $L$ is _________ (Answer in integer)
Consider the following two languages over the alphabet $\{a, b\}$ :
$$\begin{aligned} & L_1=\left\{\alpha \beta \alpha \mid \alpha \in\{a, b\}^{+} \text {AND } \beta \in\{a, b\}^{+}\right\} \\ & L_2=\left\{\alpha \beta \alpha \mid \alpha \in\{a\}^{+} \text {AND } \beta \in\{a, b\}^{+}\right\} \end{aligned}$$
Which ONE of the following statements is CORRECT?
Consider the following deterministic finite automaton (DFA) defined over the alphabet, $\Sigma=\{a, b\}$. Identify which of the following language(s) is/are accepted by the given DFA.

Consider a finite state machine (FSM) with one input $X$ and one output $f$, represented by the given state transition table. The minimum number of states required to realize this FSM is ________ . (Answer in integer)
| Present state | Next state | Output $f$ | ||
|---|---|---|---|---|
| $X = 0$ | $X = 1$ | $X = 0$ | $X = 1$ | |
| A | F | B | 0 | 0 |
| B | D | C | 0 | 0 |
| C | F | E | 0 | 0 |
| D | G | A | 1 | 0 |
| E | D | C | 0 | 0 |
| F | F | B | 1 | 1 |
| G | G | H | 0 | 1 |
| H | G | A | 1 | 0 |
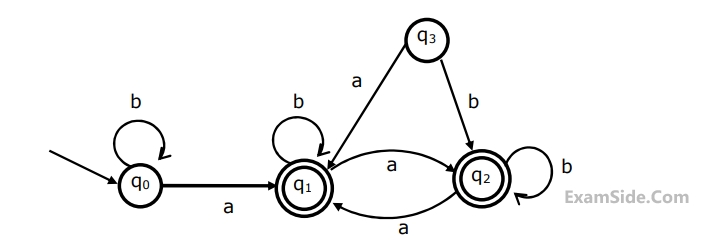
Let M be the 5-state NFA with ε-transitions shown in the diagram below.

Which one of the following regular expressions represents the language accepted by M?
Let L1 be the language represented by the regular expression b*ab*(ab*ab*)* and L2 = { w ∈ (a + b)* | |w| ≤ 4 }, where |w| denotes the length of string w. The number of strings in L2 which are also in L1 is __________.
Consider the 5-state DFA $M$ accepting the language $L(M) \subseteq (0+1)^*$ shown below. For any string $w \in (0+1)^*$ let $n_0(w)$ be the number of 0's in $w$ and $n_1(w)$ be the number of 1's in $w$.

Which of the following statements is/are FALSE?
Consider the following two regular expressions over the alphabet {0,1} :
$$r = 0^* + 1^*$$
$$s = 01^* + 10^*$$
The total number of strings of length less than or equal to 5, which are neither in r nor in s, is ________
Consider the language L over the alphabet {0, 1}, given below:
$$L = \{ w \in {\{ 0,1\} ^ * }|w$$ does not contain three or more consecutive $$1's\} $$.
The minimum number of states in a Deterministic Finite-State Automaton (DFA) for L is ___________.
Consider the following two statements about regular languages:
S1: Every infinite regular language contains an undecidable language as a subset.
S2: Every finite language is regular.
Which one of the following choices is correct?
Consider the following language.
L = { w ∈ {0, 1}* | w ends with the substring 011}
Which one of the following deterministic finite automata accepts L?
L = {x $$ \in $$ {a, b}* | number of a’s in x is divisible by 2 but not divisible by 3}
The minimum number of states in a DFA that accepts L is ______.
$${L^i} = {L^{i - 1}}.\,\,L$$ for all $$i > 0$$
The order of a language $$L$$ is defined as the smallest k such that $${L^k} = {L^{k + 1}}.$$ Consider the language $${L_1}$$ (over alphabet $$0$$) accepted by the following automaton.

The order of $${L_1}$$ is _____.

Which one of the following is TRUE?
Which one of the following is TRUE?
$$\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,$$ If all states of an $$NFA$$ are accepting states then the language accepted by the
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ $$NFA$$ is $$\sum {^ * } .$$
$$\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,$$ There exists a regular language $$A$$ such that for all languages $$B,A \cap B$$ is
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$ regular.
Which one of the following is CORRECT?

Consider the DFAs M and N given above. The number of states in a minimal DFA that accepts the language L(M) ∩ L(N) is___________.

Which one of the following sequences must follow the string 101100 so that the overall string is accepted by the automaton?
$${L_1}:\left\{ {wx{w^R}|w,x\, \in \left\{ {a,b} \right\}{}^ * } \right.$$ and $$\left. {\left| w \right|,\left| x \right| > 0} \right\},\,{w^R}$$ is the reverse of string $$w$$
$${L_2}:\left\{ {{a^n}{b^m}\left| {m \ne n} \right.} \right.$$ and $$m,n \ge \left. 0 \right\}$$
$${L_3}:\left\{ {{a^p}{b^q}{c^r}\left| {p,q,r \ge 0} \right.} \right\}$$
Which one of the following choices precisely represents the strings in $${X_0}$$?


$${L_1} = \left\{ {{0^p}{1^q}{0^r}\left| {p,q,r \ge 0} \right.} \right\}$$
$${L_2} = \left\{ {{0^p}{1^q}{0^r}\left| {p,q,r \ge 0,p \ne r} \right.} \right\}$$
Which one of the following statements is FALSE?
The missing arcs in the $$DFA$$ are

What is the minimum number of states needed in a $$DFA$$ to recognize $$L$$?

Which of the following finite state machines is a valid minimal $$DFA$$ which accepts the same languages as $$D?$$
$${L_1} = \left\{ {{a^m}{b^m}\,c\,{a^n}{b^n}\left| {m,n \ge 0} \right.} \right\}$$
$${L_2} = \left\{ {{a^i}{b^i}{c^k}\left| {i,j,k \ge 0} \right.} \right\}$$ Then $$L$$ is

The above $$DFA$$ accepts the set of all strings over $$\left\{ {0,\,\,1} \right\}$$ that


Which of the following represents the product automation $$ZY$$?






The language accepted by this automation is given by the regular expression

The minimum state automation equivalent to the above $$FSA$$ has the following number of states



Let $$S$$ denote the set of seven bit binary strings in which the first, the fourth, and the last bits are $$1$$. The number of strings in $$S$$ that are accepted by $$M$$ is

Let the language accepted by $$M$$ be $$L.$$ Let $${L_1}$$ be the language accepted by the $$NFA$$, $${M_1}$$ obtained by changing the accepting state of $$M$$ to a non accepting state and by changing the non accepting state of $$M$$ to accepting states. Which of the following statements is true?

$$L = \left. {\left\{ x \right.} \right|$$ length of $$x$$ is divisible by $$\left. 3 \right\}$$ has
$${L_1} = \left\{ {w\,w\left| {w \in {{\left\{ {a,\,b} \right\}}^ * }} \right.} \right\}$$
$${L_2} = \left\{ {w\,{w^R}\left| {w \in {{\left\{ {a,\,b} \right\}}^ * },} \right.{w^R}\,\,} \right.$$ is the reverse of $$\left. w \right\}$$
$${L_3} = \left\{ {{0^{2i}}\left| {i\,\,} \right.} \right.$$ is an integer$$\left. \, \right\}$$
$${L_4} = \left\{ {{0^{{i^2}}}\left| {i\,\,} \right.} \right.$$ is an integer$$\left. \, \right\}$$
Which of the languages are regular?

If the initial state is unknown, then the shortest input sequence to reach the final state $$C$$ is here, since initial make unknown $$m$$ $$10$$ input we can each final state $$C$$ with shortest path.
Where $$L = {\left\{ x \right.^n}{y^n}\left| {n \ge \left. 1 \right\}} \right.$$
i) $$\,\,E \to xEy\left| {xy} \right.$$
ii) $$\,\,xy\left| {\left( {{x^ + }xy{y^ + }} \right)} \right.$$
iii) $${\,\,{x^ + }{y^ + }}$$
$$L = \left\{ {xn\,{y^n}\left| {n \ge 1} \right.} \right\} - $$ generates string where equal no. of $$x$$ and equal no. of $$y's.$$
$$E \to XBy\left| {xy\,abo} \right.$$ generators tips same.
