Greedy Method · Algorithms · GATE CSE
Marks 1
Let $G$ be any undirected graph with positive edge weights, and $T$ be a minimum spanning tree of $G$. For any two vertices, $u$ and $v$, let $d_1(u, v)$ and $d_2(u, v)$ be the shortest distances between $u$ and $v$ in $G$ and $T$, respectively. Which ONE of the options is CORRECT for all possible $G, T, u$ and $v$ ?
Let G be a connected undirected weighted graph. Consider the following two statements.
S1: There exists a minimum weight edge in G which is present in every minimum spanning tree of G.
S2: If every edge in G has distinct weight, then G has a unique minimum spanning tree. Which one of the following options is correct?
Consider the following table :
| Algorithms | Design Paradigms |
|---|---|
| (P) Kruskal | (ii) Greedy |
| (Q) Quicksort | (i) Divide and Conquer |
| (R) Floyd–Warshall | (iii) Dynamic Programming |
Match the algorithms to the design paradigms they are based on.
$$P:$$ Minimum spanning tree of $$G$$ does not change
$$Q:$$ Shortest path between any pair of vertices does not change
Marks 2
Let $G$ be an edge-weighted undirected graph with positive edge weights. Suppose a positive constant $\alpha$ is added to the weight of every edge. Which ONE of the following statements is TRUE about the minimum spanning trees (MSTs) and shortest paths (SPs) in G before and after the edge weight update?
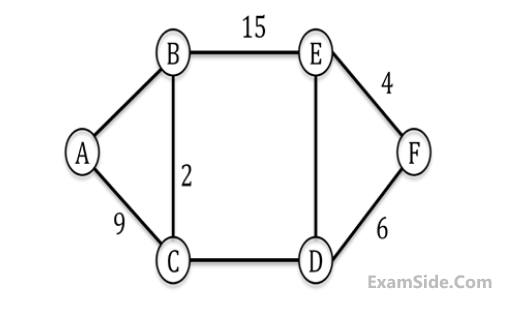
The maximum value of $x$ such that the edge between the nodes $B$ and $C$ is included in every minimum spanning tree of the given graph is _______. (Answer in integer)

Let $G$ be an undirected connected graph in which every edge has a positive integer weight. Suppose that every spanning tree in $G$ has even weight. Which of the following statements is/are TRUE for every such graph $G$?
The number of distinct minimum-weight spanning trees of the following graph is ________

Consider the string abbccddeee. Each letter in the string must be assigned a binary code satisfying the following properties:
1. For any two letters, the code assigned to one letter must not be a prefix of the code assigned to the other letter.
2. For any two letters of the same frequency, the letter which occurs earlier in the dictionary order is assigned a code whose length is at most the length of the code assigned to the other letter.
Among the set of all binary code assignments which satisfy the above two properties, what is the minimum length of the encoded string?
E = {(vi, vj) | 1 ≤ i < j ≤ 100}, and weight of the edge (vi, vj) is |i - j|. The weight of the minimum spanning tree of G is ______.
Consider the following undirected graph $$G: $$
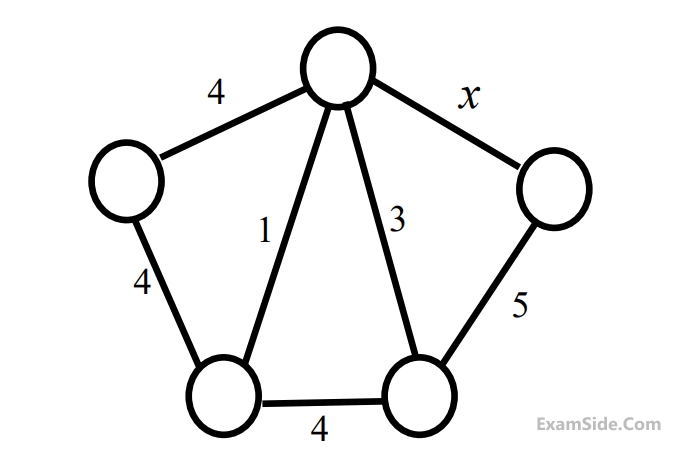
Choose a value for $$x$$ that will maximize the number of minimum weight spanning trees $$(MWSTs)$$ of $$G.$$ The number of $$MWSTs$$ of $$G$$ for this value of $$x$$ is ______.
| Item number | Weight (in Kgs) |
Value (in Rupees) |
|---|---|---|
| 1 | 10 | 60 |
| 2 | 7 | 28 |
| 3 | 4 | 20 |
| 4 | 2 | 24 |
The task is to pick a subset of these items such that their total weight is no more than $$11$$ $$Kgs$$ and their total value is maximized. Moreover, no item may be split. The total value of items picked by an optimal algorithm is denoted by $$V$$opt. A greedy algorithm sorts the items by their value-to-weight ratios in descending order and packs them greedily, starting from the first item in the ordered list. The total value of items picked by the greedy algorithm is denoted by $$V$$greedy.
The value of $$V$$opt $$−$$ $$V$$greedy is ____________.
$$\,\,\,\,\,\,\,\,\,\,{\rm I}.\,\,\,\,\,\,\,\,\,\,$$ If $$e$$ is the lightest edge of some cycle in $$G,$$ then every $$MST$$ of $$G$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$includes $$e$$
$$\,\,\,\,\,\,\,\,{\rm I}{\rm I}.\,\,\,\,\,\,\,\,\,\,$$ If $$e$$ is the heaviest edge of some cycle in $$G,$$ then every $$MST$$ of $$G$$
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,$$excludes $$e$$
The largest possible integer value of $$x,$$ for which at least one shortest path between some pair of vertices will contain the edge with weight $$x$$ is _________________.
| 1 | 2 | 5 | 14 |
|---|---|---|---|
| 3 | 4 | 6 | 23 |
| 10 | 12 | 18 | 25 |
| 31 | ∞ |
∞ | ∞ |
When an element is removed from a Young tableau, other elements should be moved into its place so that the resulting table is still a Young tableau (unfilled entries may be filled in with a $$\infty $$). The minimum number of entries (other than $$1$$) to be shifted, to remove $$1$$ from the given Young tableau is ______________.


 What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes?
What will be the cost of the minimum spanning tree (MST) of such a graph with n nodes? The length of the path from v5 to v6 in the MST of previous question with n = 10 is
The length of the path from v5 to v6 in the MST of previous question with n = 10 is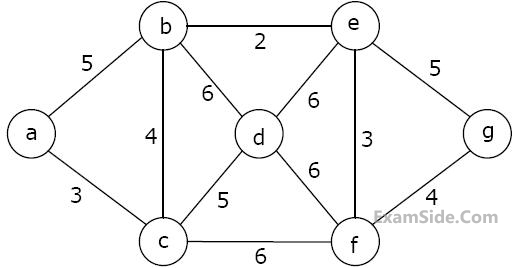 Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm?
Which one of the following is NOT the sequence of edges added to the minimum spanning tree using Kruskal’s algorithm?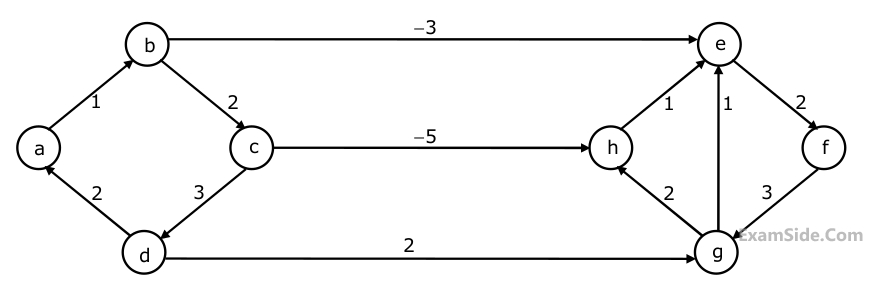 Dijkstra's single source shortest path algorithm when run from vertex a in the above graph, computes the correct shortest path distance to
Dijkstra's single source shortest path algorithm when run from vertex a in the above graph, computes the correct shortest path distance to Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm?
Which one of the following cannot be the sequence of edges added, in that order, to a minimum spanning tree using Kruskal’s algorithm? 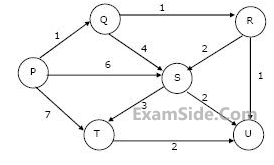 In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized?
In what order do the nodes get included into the set of vertices for which the shortest path distances are finalized?
$$$A[j,k] = \left\{ {\matrix{ {1\,if\,(j,\,k)} \cr {1\,otherwise} \cr } } \right.$$$ Consider the following algorithm.
for i = 1 to n
for j = 1 to n
for k = 1 to n
A [j , k] = max (A[j, k] (A[j, i] + A [i, k]); 