Relational Algebra · Database Management System · GATE CSE
Marks 1
Consider the following two relations, R(A, B) and S(A, C):
| R | |
|---|---|
| A | B |
| 10 | 20 |
| 20 | 30 |
| 30 | 40 |
| 30 | 50 |
| 50 | 95 |
| S | |
|---|---|
| A | C |
| 10 | 90 |
| 30 | 45 |
| 40 | 80 |
The total number of tuples obtained by evaluating the following expression
$$ \sigma_{B < C}(R \bowtie_{R.A = S.A} S) $$
is _________
Consider the following three relations in a relational database.
Employee ( $$\underline {eld} $$ , Name), Brand ( $$\underline {bld} $$ , bName), Own ( $$\underline {eld} $$ , $$\underline {bld} $$)
Which of the following relational algebra expressions return the set of elds who own all the brands?
A relation r(A, B) in a relational database has 1200 tuples. The attribute A has integer values ranging from 6 to 20, and the attribute B has integer values ranging from 1 to 20. Assume that the attributes A and B are independently distributed. The estimated number of tuples in the output of σ(A>10)∨(B=18)(r) is ______
Which of the following tuple relational calculus expression(s) is/are equivalent to $$\forall t \in r \left(P\left(t\right)\right)$$?
I. $$\neg \exists t \in r \left(P\left(t\right)\right)$$II. $$\exists t \notin r \left(P\left(t\right)\right)$$
III. $$\neg \exists t \in r \left(\neg P\left(t\right)\right)$$
IV. $$\exists t \notin r \left(\neg P\left(t\right)\right)$$
I) Relational algebra
II) Tuple relational calculus restricted to safe expressions
III) Domain relational calculus restricted to safe expressions
Let r be a relation instance with schema R = (A, B, C, D).
We define $${r_1} = {\pi _{A,B,C}}\left( r \right)$$ and $${r_1} = {\pi _{A,D}}\left( r \right)$$. Let $$s = {r_1}*{r_2}$$ where * denotes natural join. Given that the decomposition of r into r1 and r2 is lossy, which one of the following is TRUE?Select distinct a1, a2, ..., an
From r1, r2, ..., rm
Where P; Given the relations
employee (name, salary, deptno), and
department (deptno, deptname, address)
The relational algebra expression equivalent to the following tuple calculus expression:
$$\left\{ {t|t \in r \wedge \left( {t\left[ A \right] = 10 \wedge t\left[ B \right] = 20} \right)} \right\}$$ is:Marks 2
Consider two relations describing teams and players in a sports league:
$\bullet$ teams(tid, tname): tid, tname are team-id and team-name, respectively.
$\bullet$ players(pid, pname, tid): pid, pname, and tid denote player-id, player-name and the team-id of the player, respectively.
Which ONE of the following tuple relational calculus queries returns the name of the players who play for the team having tname as ' $M I$ '?
The relation schema, Person($\underline{\text{pid}}$, $city$), describes the city of residence for every person uniquely identified by $pid$. The following relational algebra operators are available: selection, projection, cross product, and rename.
To find the list of cities where at least 3 persons reside, using the above operators, the minimum number of cross product operations that must be used is
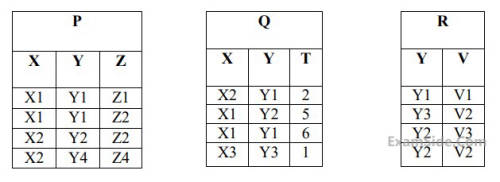
How many tuples will be returned by the following relational algebra query?
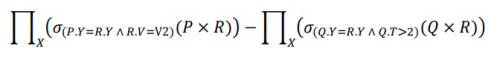
$$Q:$$ $$\,\,\,\,\,\,\,\,\,$$ $$r$$ $$\,\,\,\,$$ $$\bowtie$$ $$\,\,\,\,$$ $$\left( {{\sigma _{b < 5}}\left( s \right)} \right)$$
Let $$LOJ$$ denote the natural left outer-join operation. Assume that $$r$$ and $$s$$ contain no null values.
Which one of the following queries is NOT equivalent to $$Q$$?
Assume that $$R(A,B,C)$$ is the full natural outer join of $${R_1}$$ and $${R_2}$$. Consider the following tuples of the form $$(A,B,C): a = (1,5,null),$$ $$b = (1,null,7),$$ $$c = (3, null, 9),$$ $$d = (4,7,null),$$ $$e = (1,5,7),$$ $$f = (3,7,null),$$ $$g = (4,null,9).$$ Which one of the following statements is correct?
employee (empId, empName, empAge)
dependent (depId, eId, depName, depAge)
Consider the following relational algebra query: $$\Pi_{empId}\:(employee) - \Pi_{empId}\:(employee \bowtie_{(empId=eID) \wedge (empAge \leq depAge)} dependent)$$The above query evaluates to the set of empIds of employees whose age is greater than that of
A
| ID | Name | Age |
|---|---|---|
| 12 | Arun | 60 |
| 15 | Shreya | 24 |
| 99 | Rohit | 11 |
B
| ID | Name | Age |
|---|---|---|
| 15 | Shreya | 24 |
| 25 | Hari | 40 |
| 98 | Rohit | 20 |
| 99 | Rohit | 11 |
C
| ID | Phone | Area |
|---|---|---|
| 10 | 2200 | 02 |
| 99 | 2100 | 01 |
How many tuples does the result of the following SQL query contain?
SELECT A.Id
FROM A
WHERE A.Age > ALL (SELECT B.Age
FROM B
WHERE B.Name = 'Arun')A
| ID | Name | Age |
|---|---|---|
| 12 | Arun | 60 |
| 15 | Shreya | 24 |
| 99 | Rohit | 11 |
B
| ID | Name | Age |
|---|---|---|
| 15 | Shreya | 24 |
| 25 | Hari | 40 |
| 98 | Rohit | 20 |
| 99 | Rohit | 11 |
C
| ID | Phone | Area |
|---|---|---|
| 10 | 2200 | 02 |
| 99 | 2100 | 01 |
How many tuples does the result of the following relational algebra expression contain? Assume that the schema of A ∪ B is the same as that of A. $$(A\cup B)\bowtie _{A.Id > 40 \vee C.Id < 15} C$$
$$Q1: \pi_{A_1, \dots ,A_p} \left(\sigma_{A_p=c}\left(r\right)\right)$$ where is a constant
$$Q2: \pi_{A_1, \dots ,A_p} \left(\sigma_{c_1 \leq A_p \leq c_2}\left(r\right)\right)$$ where c1 and c2 are constants
The database can be configured to do ordered indexing on Ap or hashing on Ap. Which of the following statements is TRUE?
The relation R contains 200 tuples and the relation S contains 100 tuples. What is the maximum number of tuples possible in the natural join R $$\Join$$ S?
R (P, Q, R1, R2, R3)
S (P, Q, S1, S2)
Where {P, Q} is the key for both schemas. Which of the following queries are equivalent?I. $$\Pi_P \left(R \bowtie S\right)$$
II. $$\Pi_P \left(R\right) \bowtie \Pi_P\left(S\right)$$
III. $$\Pi_P \left(\Pi_{P, Q} \left(R\right) \cap \Pi_{P,Q} \left(S\right) \right)$$
IV. $$\Pi_P \left(\Pi_{P, Q} \left(R\right) - \left(\Pi_{P,Q} \left(R\right) - \Pi_{P,Q} \left(S\right)\right)\right)$$
b-Schema = (b-name, b-city, assets)
a-Schema = (a-num, b-name, bal)
d-Schema = (c-name, a-number)
Let branch, account and depositor be respectively instances of the above schemas. Assume that account and depositor relations are much bigger than the branch relation.
Consider the following query:Пc-name (σb-city = “Agra” ⋀ bal < 0 (branch $$ \Join $$ (account $$ \Join $$ depositor))
Which one of the following queries is the most efficient version of the above query ?
Consider the relation employee(name, sex, supervisorName) with name as the key, supervisorName gives the name of the supervisor of the employee under consideration. What does the following Tuple Relational Calculus query produce?
$$\eqalign{ & \{ e.name\,|\,employee(e) \wedge \cr & (\forall x)[\neg employee(x) \vee \cr & x.\sup ervisorName \ne e.name\, \vee \cr & x.sex = 'male']\} \cr} $$Information about a collection of students is given by the relation studInfo(studId, name, sex). The relation enroll(studId, courseId) gives which student has enrolled for (or taken) what course(s). Assume that every course is taken by at least one male and at least one female student. What does the following relational algebra expression represent?
$$\eqalign{ & \prod\nolimits_{courseId} {((\prod\nolimits_{studId} {({\sigma _{sex = 'female'}}} } \cr & (studInfo)) \times \prod\nolimits_{courseId} {(enroll)) - enroll)} \cr} $$Table: student
| Roll | Name | Hostel | Marks |
|---|---|---|---|
| 1798 | Manoj Rathod | 7 | 95 |
| 2154 | Soumic Banerjee | 5 | 68 |
| 2369 | Gumma Reddy | 7 | 86 |
| 2581 | Pradeep Pendse | 6 | 92 |
| 2643 | Suhas Kulkarni | 5 | 78 |
| 2711 | Nitin Kadam | 8 | 72 |
| 2872 | Kiran Vora | 5 | 92 |
| 2926 | Manoj Kunkalikar |
5 | 94 |
| 2959 | Hemant Karkhanis |
7 | 88 |
| 3125 | Rajesh Doshi | 5 | 82 |
Table: hobby
| Roll | Hobbyname |
|---|---|
| 1798 | chess |
| 1798 | music |
| 2154 | music |
| 2369 | swimming |
| 2581 | cricket |
| 2643 | chess |
| 2643 | hockey |
| 2711 | volleyball |
| 2872 | football |
| 2926 | cricket |
| 2959 | photography |
| 3125 | music |
| 3125 | chess |
The following SQL query is executed on the above tables:
Select hostel
From student natural join hobby
Where marks > = 75 and roll between 2000 and 3000;Relations S and H with the same schema as those of these two tables respectively contain the same information as tuples. A new relation S’ is obtained by the following relational algebra operation:
$$\eqalign{ & S' = \prod\nolimits_{hostel} {(({\sigma _{S.roll = H.roll}}} \cr & ({\sigma _{marks > 75\,\,\,and\,\,roll > 2000\,\,and\,\,roll < 3000}}(S))X(H)) \cr} $$The difference between the number of rows output by the SQL statement and the number of tuples in S’ is
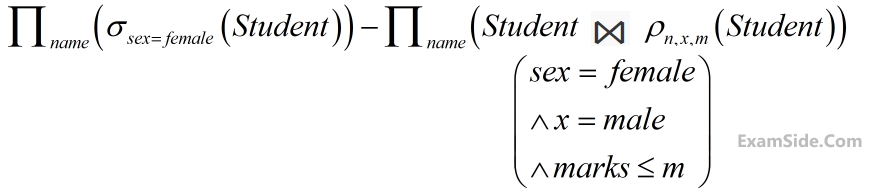
A library relational database system uses the following schema
USERS (User #, User Name, Home Town)
BOOKS (Books # Book Title, Author Name)
ISSUED (Book #, User #, Date)
Explain in one English sentence, what each of the following relational algebra queries is designed to determine.(a) $$\sigma_{ \text{User#}=6}\left(\pi_{\text{User#, Book Title}}\left(\left(\text{USERS} \bowtie \text{ISSUED}\right) \bowtie \text{BOOKS}\right)\right)$$
(b) $$\pi_{\text{Author Name}}\left(\text{BOOKS} \bowtie \sigma_{\text{Home Town=Delhi}} \left(\text{USERS} \bowtie \text{ISSUED}\right)\right)$$