Linked List · Data Structures · GATE CSE

Let SLLdel be a function that deletes a node in a singly-linked list given a pointer to the node and a pointer to the head of the list. Similarly, let DLLdel be another function that deletes a node in a doubly-linked list given a pointer to the node and a pointer to the head of the list.

Let $$n$$ denote the number of nodes in each of the linked lists. Which one of the following choices is TRUE about the worst-case time complexity of SLLdel and DLLdel?

Consider the problem of reversing a singly linked list. To take an example, given the linked list below:

the reversed linked list should look like

Which one of the following statements is TRUE about the time complexity of algorithms that solve the above problem in O(1) space?

What is the worst case time complexity of inserting n elements into an empty linked list, if the linked list needs to be maintained in sorted order?

$$N$$ items are stored in a sorted doubly linked list. For a $$delete$$ operation, a pointer is provided to the record to be deleted. For a $$decrease$$-$$key$$ operation, a pointer is provided to the record on which the operation is to be performed.

An algorithm performs the following operations on the list in this order:
$$\Theta \left( N \right),\,\,delete,\,\,O\left( {\log N} \right)\,insert,\,$$ $$\,O\left( {\log N} \right)\,fund, and $$ $$\Theta \left( N \right)\,$$ $$decrease$$-$$key.$$ What is the time complexity of all these operations put together?

Let P be a singly linked list, Let Q be the pointer to an intermediate node x in the list.What is the worst-case time complexity of the best known algorithm to delete the node x from the list?

In the worst case, the number of comparisons needed to search a singly linked list of length n for a given element is

Let LIST be a datatype for an implementation of linked list defined as follows:

typedef struct list {
    int data;
    struct list *next;
} LIST;

Suppose a program has created two linked lists, L1 and L2, whose contents are given in the figure below (code for creating L1 and L2 is not provided here). L1 contains 9 nodes, and L2 contains 7 nodes. Consider the following C program segment that modifies the list L1. The number of nodes that will be there in L1 after the execution of the code segment is _________. (Answer in integer)

A queue is implemented using a non-circular singly linked list. The queue has a head pointer and a tail pointer, as shown in the figure. Let $$n$$ denote the number of nodes in the queue. Let $$enqueue$$ be implemented by inserting a new node at the head, and $$dequeue$$ be implemented by deletion of a node from the tail.

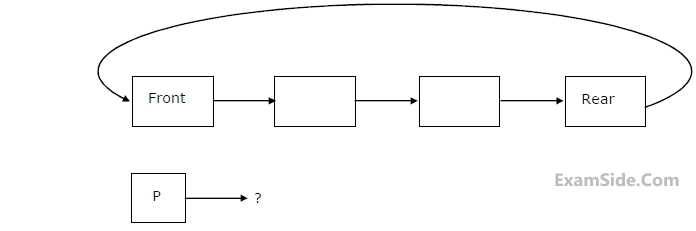
Which one of the following is the time complexity of the most time-efficient implementation of $$enqueue$$ and $$dequeue,$$ respectively, for this data structure?

The preorder traversal sequence of a binary search tree is 30, 20, 10, 15, 25, 23, 39, 35, 42. Which one of the following is the postorder traversal sequence of the same tree?

The following C function takes a simply-linked list as input argument. It modifies the list by moving the last element to the front of the list and returns the modified list. Some part of the code is left blank.

typedef struct node { 
    int value; 
    struct node *next; 
} Node;
 
Node *move_to_front(Node *head) { 
     Node *p, *q; 
     if ((head = = NULL: || (head->next = = NULL)) return head; 
     q = NULL; p = head; 
     while (p-> next !=NULL) { 
       q=P; 
       p=p->next; 
     } 
     return head; 
} 

Choose the correct alternative to replace the blank line.

The following C function takes a single-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1,2,3,4,5,6,7 in the given order. What will be the contents of the list after the function completes execution?

struct node { 
    int value; 
    struct node *next; 
}; 

Void rearrange (struct node *list ){ 
    struct node *p, * q; 
    int temp; 
    if( !list || !list-> next) return; 
    p = list; q = list->next; 
    while (q) { 
      temp = p->value; 
      p-> value = q ->value; 
      q-> value = temp; 
      p = q-> next; 
      q = p ? p->next : 0; 
    } 
}

The following C function takes a single-linked list of integers as a parameter and rearranges the elements of the list. The function is called with the list containing the integers 1,2,3,4,5,6,7 in the given order. What will be the contents of the list after the function completes execution?

struct node { 
    int value; 
    struct node *next; 
}; 

Void rearrange (struct node *list ){ 
    struct node *p, * q; 
    int temp; 
    if( !list || !list-> next) return; 
    p = list; q = list->next; 
    while (q) { 
      temp = p->value; 
      p-> value = q ->value; 
      q-> value = temp; 
      p = q-> next; 
      q = p ? p->next : 0; 
    } 
}

A circularly linked list is used to represent a Queue. A single variable p is used to access the Queue. To which node should p point such that both the operations enQueue and deQueue can be performed in constant time?

Consider the function f defined below.

struct item { 
      int data; 
      struct item * next; 
}; 

int f(struct item *p) { 
      return ((p == NULL) || (p ->next == NULL) || 
        ((p->data <= p -> next -> data) && 
        f(p-> next))); 
}

For a given linked list p, the function f returns 1 if and only if

Linked lists are not suitable data structures of which one of the following problems?

In a circular linked list organization,insertion of a record involves modification of :