A ball is thrown from the location $\left(x_0, y_0\right)=(0,0)$ of a horizontal playground with an initial speed $v_0$ at an angle $\theta_0$ from the $+x$-direction. The ball is to be hit by a stone, which is thrown at the same time from the location $\left(x_1, y_1\right)=(L, 0)$. The stone is thrown at an angle $\left(180-\theta_1\right)$ from the $+x$-direction with a suitable initial speed. For a fixed $v_0$, when $\left(\theta_0, \theta_1\right)=\left(45^{\circ}, 45^{\circ}\right)$, the stone hits the ball after time $T_1$, and when $\left(\theta_0, \theta_1\right)=\left(60^{\circ}, 30^{\circ}\right)$, it hits the ball after time $T_2$. In such a case, $\left(T_1 / T_2\right)^2$ is ______.

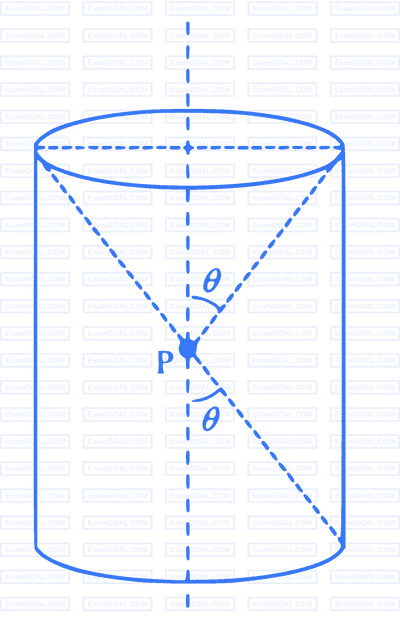
A charge is kept at the central point $\mathrm{P}$ of a cylindrical region. The two edges subtend a half-angle $\theta$ at $\mathrm{P}$, as shown in the figure. When $\theta=30^{\circ}$, then the electric flux through the curved surface of the cylinder is $\Phi$. If $\theta=60^{\circ}$, then the electric flux through the curved surface becomes $\Phi / \sqrt{n}$, where the value of $n$ is ___.

Two equilateral-triangular prisms $\mathrm{P}_1$ and $\mathrm{P}_2$ are kept with their sides parallel to each other, in vacuum, as shown in the figure. A light ray enters prism $\mathrm{P}_1$ at an angle of incidence $\theta$ such that the outgoing ray undergoes minimum deviation in prism $\mathrm{P}_2$. If the respective refractive indices of $\mathrm{P}_1$ and $\mathrm{P}_2$ are $\sqrt{\frac{3}{2}}$ and $\sqrt{3}$, then $\theta=\sin ^{-1}\left[\sqrt{\frac{3}{2}} \sin \left(\frac{\pi}{\beta}\right)\right]$, where the value of $\beta$ is ____.

An infinitely long thin wire, having a uniform charge density per unit length of $5 \mathrm{nC} / \mathrm{m}$, is passing through a spherical shell of radius $1 \mathrm{~m}$, as shown in the figure. A $10 \mathrm{nC}$ charge is distributed uniformly over the spherical shell. If the configuration of the charges remains static, the magnitude of the potential difference between points $\mathrm{P}$ and $\mathrm{R}$, in Volt, is ________.

[Given: In SI units $\frac{1}{4 \pi \epsilon_0}=9 \times 10^9, \ln 2=0.7$. Ignore the area pierced by the wire.]