A positive, singly ionized atom of mass number $A_{\mathrm{M}}$ is accelerated from rest by the voltage $192 \mathrm{~V}$. Thereafter, it enters a rectangular region of width $w$ with magnetic field $\vec{B}_0=0.1 \hat{k}$ Tesla, as shown in the figure. The ion finally hits a detector at the distance $x$ below its starting trajectory.

[Given: Mass of neutron/proton $=(5 / 3) \times 10^{-27} \mathrm{~kg}$, charge of the electron $=1.6 \times 10^{-19} \mathrm{C}$.]

Which of the following option(s) is(are) correct?

The dimensions of a cone are measured using a scale with a least count of $2 \mathrm{~mm}$. The diameter of the base and the height are both measured to be $20.0 \mathrm{~cm}$. The maximum percentage error in the determination of the volume is _______.

A ball is thrown from the location $\left(x_0, y_0\right)=(0,0)$ of a horizontal playground with an initial speed $v_0$ at an angle $\theta_0$ from the $+x$-direction. The ball is to be hit by a stone, which is thrown at the same time from the location $\left(x_1, y_1\right)=(L, 0)$. The stone is thrown at an angle $\left(180-\theta_1\right)$ from the $+x$-direction with a suitable initial speed. For a fixed $v_0$, when $\left(\theta_0, \theta_1\right)=\left(45^{\circ}, 45^{\circ}\right)$, the stone hits the ball after time $T_1$, and when $\left(\theta_0, \theta_1\right)=\left(60^{\circ}, 30^{\circ}\right)$, it hits the ball after time $T_2$. In such a case, $\left(T_1 / T_2\right)^2$ is ______.

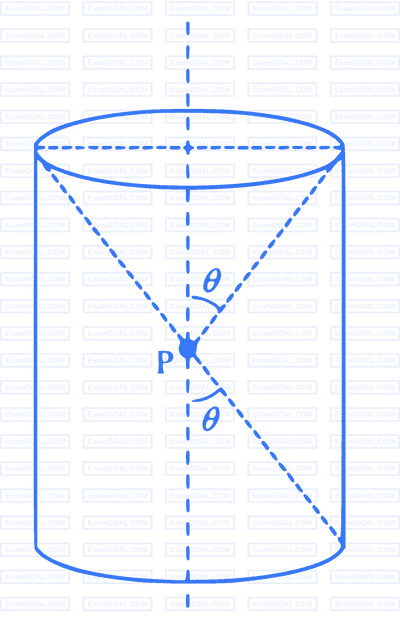
A charge is kept at the central point $\mathrm{P}$ of a cylindrical region. The two edges subtend a half-angle $\theta$ at $\mathrm{P}$, as shown in the figure. When $\theta=30^{\circ}$, then the electric flux through the curved surface of the cylinder is $\Phi$. If $\theta=60^{\circ}$, then the electric flux through the curved surface becomes $\Phi / \sqrt{n}$, where the value of $n$ is ___.