On a frictionless horizontal plane, a bob of mass $m=0.1 \mathrm{~kg}$ is attached to a spring with natural length $l_{0}=0.1 \mathrm{~m}$. The spring constant is $k_{1}=0.009 \,\mathrm{Nm}^{-1}$ when the length of the spring $l>l_{0}$ and is $k_{2}=0.016 \,\mathrm{Nm}^{-1}$ when $l < l_{0}$. Initially the bob is released from $l=$ $0.15 \mathrm{~m}$. Assume that Hooke's law remains valid throughout the motion. If the time period of the full oscillation is $T=(n \pi) s$, then the integer closest to $n$ is __________.

An object and a concave mirror of focal length $f=10 \mathrm{~cm}$ both move along the principal axis of the mirror with constant speeds. The object moves with speed $V_{0}=15 \mathrm{~cm} \mathrm{~s}^{-1}$ towards the mirror with respect to a laboratory frame. The distance between the object and the mirror at a given moment is denoted by $u$. When $u=30 \mathrm{~cm}$, the speed of the mirror $V_{m}$ is such that the image is instantaneously at rest with respect to the laboratory frame, and the object forms a real image. The magnitude of $V_{m}$ is _________ $\mathrm{cm} \,\mathrm{s}^{-1}$.

In the figure, the inner (shaded) region $A$ represents a sphere of radius $r_{A}=1$, within which the electrostatic charge density varies with the radial distance $r$ from the center as $\rho_{A}=k r$, where $k$ is positive. In the spherical shell $B$ of outer radius $r_{B}$, the electrostatic charge density varies as $\rho_{B}=$ $\frac{2 k}{r}$. Assume that dimensions are taken care of. All physical quantities are in their SI units.

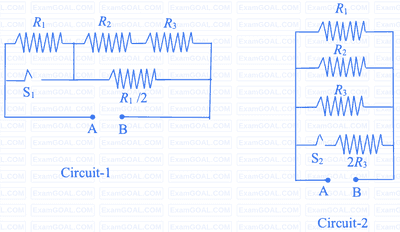
Which of the following statement(s) is(are) correct?