If the electron in hydrogen atom jumps from third Bohr orbit to ground state directly and the difference between energies of the two states is radiated in the form of photons. If the work function of the material is 4.1 eV , then stopping potential is nearly

[Energy of electron in $n^{\text {th }}$ orbit $=\frac{-13 \cdot 6}{n^2} \mathrm{eV}$ ]

When a metal surface is illuminated by light of wavelength $\lambda_1$ and $\lambda_2$, the maximum velocities of photoelectrons ejected are V and 2 V respectively. The work function of the metal is ( $\mathrm{h}=$ Planck's constant, $\mathrm{c}=$ velocity of light, $\lambda_1>\lambda_2$ )

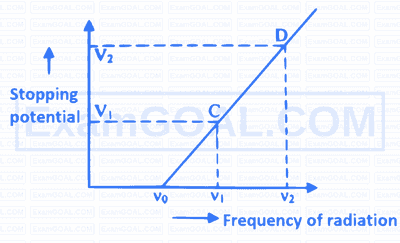
Graph shows variation of stopping potential with frequency of incident radiation on a metal plate. The value of Planck's constant is [ $\mathrm{e}=$ charge on photoelectron]