JEE Advanced 2017 Paper 2 Offline | Magnetism Question 14 | Physics

1

JEE Advanced 2017 Paper 2 Offline

MCQ (Single Correct Answer)

+3

-0.75

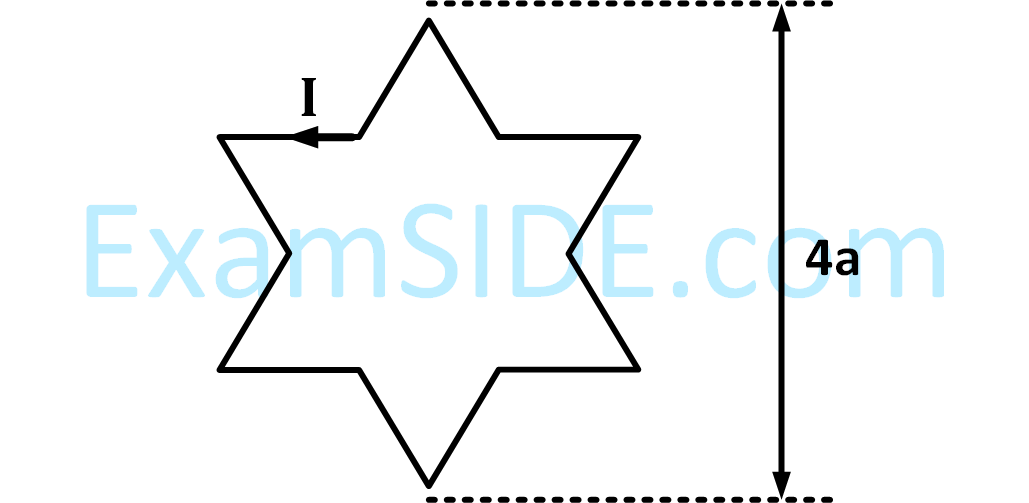
A symmetric star shaped conducting wire loop is carrying a steady state current $${\rm I}$$ as shown in the figure. The distance between the diametrically opposite vertices of the star is $$4a.$$ The magnitude of the magnetic field at the center of the loop is

JEE Advanced 2017 Paper 2 Offline Physics - Magnetism Question 37 English

JEE Advanced 2017 Paper 2 Offline Physics - Magnetism Question 37 English

A

$${{{\mu _0}1} \over {4\pi a}}6\left[ {\sqrt 3 - 1} \right]$$

B

$${{{\mu _0}1} \over {4\pi a}}6\left[ {\sqrt 3 + 1} \right]$$

C

$${{{\mu _0}1} \over {4\pi a}}3\left[ {\sqrt 3 - 1} \right]$$

D

$${{{\mu _0}1} \over {4\pi a}}3\left[ {2 - \sqrt 3 } \right]$$

2

JEE Advanced 2017 Paper 1 Offline

MCQ (Single Correct Answer)

+3

-0.75

A charged particle (electron or proton) is introduced at the origin (x=0,y=0,z=0) with a given initial velocity $$\overrightarrow v .$$ A uniform electric field $$\overrightarrow E $$ and a uniform magnetic field $$\overrightarrow B $$ exist everywhere. The velocity $$\overrightarrow v ,$$ electric field $$\overrightarrow E $$ and magnetic field $$\overrightarrow B $$ are given in column $$1,2$$ and $$3,$$ respectively. The quantities $${E_0},{B_0}$$ are positive in magnitude.

Column 1		Column 2		Column 3
(I)	Electron with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(i)	$$\overrightarrow E = {E_0}\widehat z$$	(P)	$$\overrightarrow B = - {B_0}\widehat x$$
(II)	Electron with $$\overrightarrow v = {{{E_0}} \over {{B_0}}}\widehat y$$	(ii)	$$\overrightarrow E = - {E_0}\widehat y$$	(Q)	$$\overrightarrow B = {B_0}\widehat x$$
(III)	Proton with $$\overrightarrow v = 0$$	(iii)	$$\overrightarrow E = - {E_0}\widehat x$$	(R)	$$\overrightarrow B = {B_0}\widehat y$$
(IV)	Proton with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(iv)	$$\overrightarrow E = {E_0}\widehat x$$	(S)	$$\overrightarrow B = {B_0}\widehat z$$

In which case will the particle move in a straight line with constant velocity?

A

$$\left( {{\rm I}{\rm I}{\rm I}} \right)\left( {ii} \right)\left( R \right)$$

B

$$\left( {{\rm I}V} \right)\left( i \right)\left( S \right)$$

C

$$\left( {{\rm I}{\rm I}{\rm I}} \right)\left( {iii} \right)\left( P \right)$$

D

$$\left( {{\rm I}{\rm I}} \right)\left( {iii} \right)\left( S \right)$$

3

JEE Advanced 2017 Paper 1 Offline

MCQ (Single Correct Answer)

+3

-0.75

A charged particle (electron or proton) is introduced at the origin (x=0,y=0,z=0) with a given initial velocity $$\overrightarrow v .$$ A uniform electric field $$\overrightarrow E $$ and a uniform magnetic field $$\overrightarrow B $$ exist everywhere. The velocity $$\overrightarrow v ,$$ electric field $$\overrightarrow E $$ and magnetic field $$\overrightarrow B $$ are given in column $$1,2$$ and $$3,$$ respectively. The quantities $${E_0},{B_0}$$ are positive in magnitude.

Column 1		Column 2		Column 3
(I)	Electron with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(i)	$$\overrightarrow E = {E_0}\widehat z$$	(P)	$$\overrightarrow B = - {B_0}\widehat x$$
(II)	Electron with $$\overrightarrow v = {{{E_0}} \over {{B_0}}}\widehat y$$	(ii)	$$\overrightarrow E = - {E_0}\widehat y$$	(Q)	$$\overrightarrow B = {B_0}\widehat x$$
(III)	Proton with $$\overrightarrow v = 0$$	(iii)	$$\overrightarrow E = - {E_0}\widehat x$$	(R)	$$\overrightarrow B = {B_0}\widehat y$$
(IV)	Proton with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(iv)	$$\overrightarrow E = {E_0}\widehat x$$	(S)	$$\overrightarrow B = {B_0}\widehat z$$

In which case will the particle describe a helical path with axis along the positive $$z$$ direction?

A

$$\left( {{\rm I}V} \right)\left( i \right)\left( S \right)$$

B

$$\left( {{\rm I}{\rm I}} \right)\left( {ii} \right)\left( R \right)$$

C

$$\left( {{\rm I}{\rm I}{\rm I}} \right)\left( {iii} \right)\left( P \right)$$

D

$$\left( {{\rm I}V} \right)\left( {ii} \right)\left( R \right)$$

4

JEE Advanced 2017 Paper 1 Offline

MCQ (Single Correct Answer)

+3

-0.75

A charged particle (electron or proton) is introduced at the origin (x=0,y=0,z=0) with a given initial velocity $$\overrightarrow v .$$ A uniform electric field $$\overrightarrow E $$ and a uniform magnetic field $$\overrightarrow B $$ exist everywhere. The velocity $$\overrightarrow v ,$$ electric field $$\overrightarrow E $$ and magnetic field $$\overrightarrow B $$ are given in column $$1,2$$ and $$3,$$ respectively. The quantities $${E_0},{B_0}$$ are positive in magnitude.

Column 1		Column 2		Column 3
(I)	Electron with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(i)	$$\overrightarrow E = {E_0}\widehat z$$	(P)	$$\overrightarrow B = - {B_0}\widehat x$$
(II)	Electron with $$\overrightarrow v = {{{E_0}} \over {{B_0}}}\widehat y$$	(ii)	$$\overrightarrow E = - {E_0}\widehat y$$	(Q)	$$\overrightarrow B = {B_0}\widehat x$$
(III)	Proton with $$\overrightarrow v = 0$$	(iii)	$$\overrightarrow E = - {E_0}\widehat x$$	(R)	$$\overrightarrow B = {B_0}\widehat y$$
(IV)	Proton with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(iv)	$$\overrightarrow E = {E_0}\widehat x$$	(S)	$$\overrightarrow B = {B_0}\widehat z$$

In which case would the particle move in a straight line along the negative direction of $$y$$-axis (i.e., move along $$ - \widehat y$$)?

A

$$\left( {{\rm I}{\rm I}} \right)\left( {iii} \right)\left( Q \right)$$

B

$$\left( {{\rm I}{\rm I}{\rm I}} \right)\left( {ii} \right)\left( R \right)$$

C

$$\left( {{\rm I}V} \right)\left( {ii} \right)\left( S \right)$$

D

$$\left( {{\rm I}{\rm I}{\rm I}} \right)\left( {ii} \right)\left( P \right)$$