A circular coil of radius R and N turns has negligible resistance. As shown in the schematic figure, its two ends are connected to two wires and it is hanging by those wires with its plane being vertical. The wires are connected to a capacitor with charge Q through a switch. The coil is in a horizontal uniform magnetic field Bo parallel to the plane of the coil. When the switch is closed, the capacitor gets discharged through the coil in a very short time. By the time the capacitor is discharged fully, magnitude of the angular momentum gained by the coil will be (assume that the discharge time is so short that the coil has hardly rotated during this time)

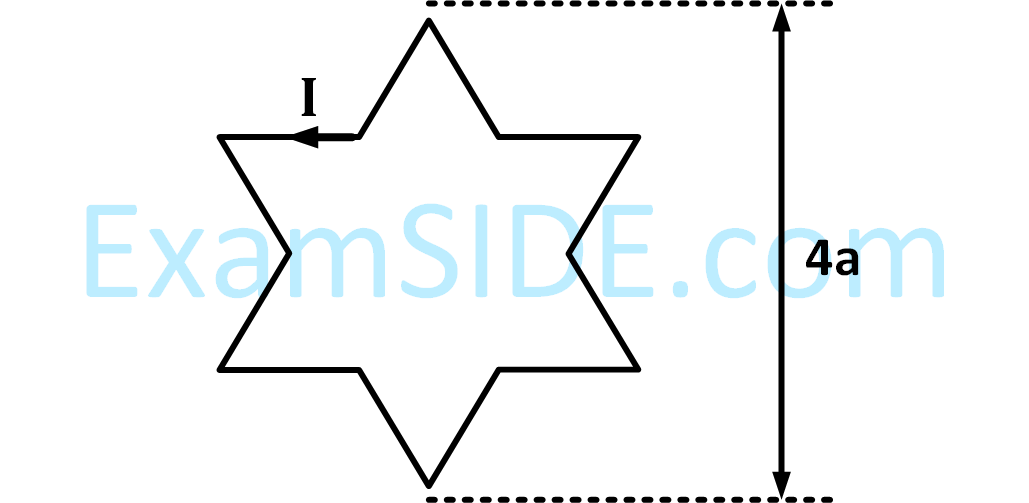
A symmetric star shaped conducting wire loop is carrying a steady state current $${\rm I}$$ as shown in the figure. The distance between the diametrically opposite vertices of the star is $$4a.$$ The magnitude of the magnetic field at the center of the loop is

A charged particle (electron or proton) is introduced at the origin (x=0,y=0,z=0) with a given initial velocity $$\overrightarrow v .$$ A uniform electric field $$\overrightarrow E $$ and a uniform magnetic field $$\overrightarrow B $$ exist everywhere. The velocity $$\overrightarrow v ,$$ electric field $$\overrightarrow E $$ and magnetic field $$\overrightarrow B $$ are given in column $$1,2$$ and $$3,$$ respectively. The quantities $${E_0},{B_0}$$ are positive in magnitude.

Column 1		Column 2		Column 3
(I)	Electron with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(i)	$$\overrightarrow E = {E_0}\widehat z$$	(P)	$$\overrightarrow B = - {B_0}\widehat x$$
(II)	Electron with $$\overrightarrow v = {{{E_0}} \over {{B_0}}}\widehat y$$	(ii)	$$\overrightarrow E = - {E_0}\widehat y$$	(Q)	$$\overrightarrow B = {B_0}\widehat x$$
(III)	Proton with $$\overrightarrow v = 0$$	(iii)	$$\overrightarrow E = - {E_0}\widehat x$$	(R)	$$\overrightarrow B = {B_0}\widehat y$$
(IV)	Proton with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(iv)	$$\overrightarrow E = {E_0}\widehat x$$	(S)	$$\overrightarrow B = {B_0}\widehat z$$

In which case will the particle move in a straight line with constant velocity?

A charged particle (electron or proton) is introduced at the origin (x=0,y=0,z=0) with a given initial velocity $$\overrightarrow v .$$ A uniform electric field $$\overrightarrow E $$ and a uniform magnetic field $$\overrightarrow B $$ exist everywhere. The velocity $$\overrightarrow v ,$$ electric field $$\overrightarrow E $$ and magnetic field $$\overrightarrow B $$ are given in column $$1,2$$ and $$3,$$ respectively. The quantities $${E_0},{B_0}$$ are positive in magnitude.

Column 1		Column 2		Column 3
(I)	Electron with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(i)	$$\overrightarrow E = {E_0}\widehat z$$	(P)	$$\overrightarrow B = - {B_0}\widehat x$$
(II)	Electron with $$\overrightarrow v = {{{E_0}} \over {{B_0}}}\widehat y$$	(ii)	$$\overrightarrow E = - {E_0}\widehat y$$	(Q)	$$\overrightarrow B = {B_0}\widehat x$$
(III)	Proton with $$\overrightarrow v = 0$$	(iii)	$$\overrightarrow E = - {E_0}\widehat x$$	(R)	$$\overrightarrow B = {B_0}\widehat y$$
(IV)	Proton with $$\overrightarrow v = 2{{{E_0}} \over {{B_0}}}\widehat x$$	(iv)	$$\overrightarrow E = {E_0}\widehat x$$	(S)	$$\overrightarrow B = {B_0}\widehat z$$

In which case will the particle describe a helical path with axis along the positive $$z$$ direction?