1
JEE Advanced 2013 Paper 1 Offline
Numerical
+4
-0
A bob of mass m, suspended by a string of length l1 is given a minimum velocity required to complete a full circle in the vertical plane. At the highest point, it collides elastically with another bob of mass m suspended by a string of length l2, which is initially at rest. Both the strings are mass-less and inextensible. If the second bob, after collision acquires the minimum speed required to complete a full circle in the vertical plane, the ratio $${{{l_1}} \over {{l_2}}}$$ is
Your input ____
2
JEE Advanced 2013 Paper 1 Offline
Numerical
+4
-0
A particle of mass 0.2 kg is moving in one dimension under a force that delivers a constant power 0.5 W to
the particle. If the initial speed (in m/s) of the particle is zero, the speed (in m/s) after 5 s is
Your input ____
3
IIT-JEE 2011 Paper 2 Offline
Numerical
+4
-0
A block of mass 0.18 kg is attached to a spring of force-constant 2 N/m. The coefficient of friction between the block and the floor is 0.1. Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06 m and comes to rest for the first time. The initial velocity of the block in m/s is V = N/10. Then N is

Your input ____
4
IIT-JEE 2009 Paper 2 Offline
Numerical
+3
-1
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.
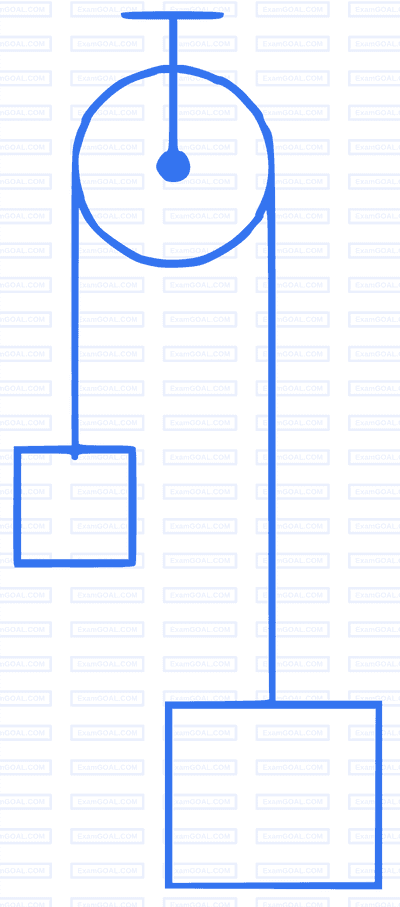
Your input ____
Questions Asked from Work Power & Energy (Numerical)
Number in Brackets after Paper Indicates No. of Questions
JEE Advanced Subjects
Physics
Mechanics
Units & Measurements Motion Laws of Motion Work Power & Energy Impulse & Momentum Rotational Motion Properties of Matter Heat and Thermodynamics Simple Harmonic Motion Waves Gravitation
Electricity
Electrostatics Current Electricity Capacitor Magnetism Electromagnetic Induction Alternating Current Electromagnetic Waves
Optics
Modern Physics
Chemistry
Physical Chemistry
Some Basic Concepts of Chemistry Structure of Atom Redox Reactions Gaseous State Chemical Equilibrium Ionic Equilibrium Solutions Thermodynamics Chemical Kinetics and Nuclear Chemistry Electrochemistry Solid State Surface Chemistry
Inorganic Chemistry
Periodic Table & Periodicity Chemical Bonding & Molecular Structure Isolation of Elements Hydrogen s-Block Elements p-Block Elements d and f Block Elements Coordination Compounds Salt Analysis
Organic Chemistry
Mathematics
Algebra
Quadratic Equation and Inequalities Sequences and Series Mathematical Induction and Binomial Theorem Matrices and Determinants Permutations and Combinations Probability Vector Algebra 3D Geometry Statistics Complex Numbers
Trigonometry
Coordinate Geometry
Calculus