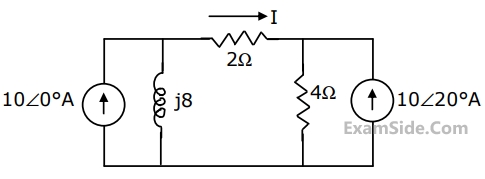
For the network shown in Fig., evaluate the current I flowing through the 2Ω resistor using superposition theorem.
A voltage source of internal impedance $${\mathrm R}_\mathrm s\;+\;{\mathrm{jX}}_\mathrm s$$ supplies power to a load of impedance $${\mathrm R}_\mathrm L\;+\;{\mathrm{jX}}_\mathrm L$$ in which only $${\mathrm R}_\mathrm L$$ is variable. Determine the value of $${\mathrm R}_\mathrm L$$ for maximum power transfer from the source to the load. Also, find the numerical value of $${\mathrm R}_\mathrm L$$ if the source impedance is 3.0 Ω (purely resistive) and $${\mathrm X}_\mathrm L$$ is 4.0 Ω.
In the circuit of Fig. when R = 0 Ω, the current iR equals 10 A.
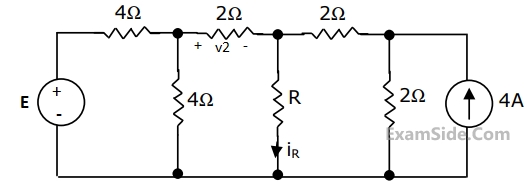
(a) Find the value of R for which it absorbs maximum power.
(b) Find the value of E.
(c) Find v2 when R = $$\infty$$ ( open circuit)
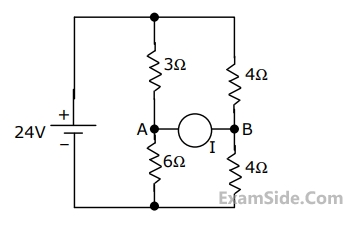
In the circuit shown in Fig., it is known that the variable current source I absorbs power.Find I (in magnitude and direction) so that it receives maximum power and also find the amount of power absorbed by it.