A voltage source of internal impedance $${\mathrm R}_\mathrm s\;+\;{\mathrm{jX}}_\mathrm s$$ supplies power to a load of impedance $${\mathrm R}_\mathrm L\;+\;{\mathrm{jX}}_\mathrm L$$ in which only $${\mathrm R}_\mathrm L$$ is variable. Determine the value of $${\mathrm R}_\mathrm L$$ for maximum power transfer from the source to the load. Also, find the numerical value of $${\mathrm R}_\mathrm L$$ if the source impedance is 3.0 Ω (purely resistive) and $${\mathrm X}_\mathrm L$$ is 4.0 Ω.
In the circuit of Fig. when R = 0 Ω, the current iR equals 10 A.
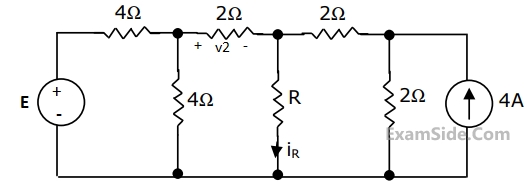
(a) Find the value of R for which it absorbs maximum power.
(b) Find the value of E.
(c) Find v2 when R = $$\infty$$ ( open circuit)
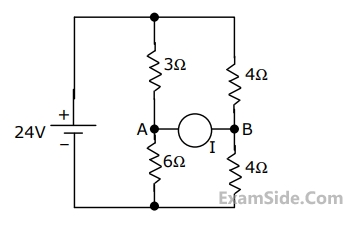
In the circuit shown in Fig., it is known that the variable current source I absorbs power.Find I (in magnitude and direction) so that it receives maximum power and also find the amount of power absorbed by it.
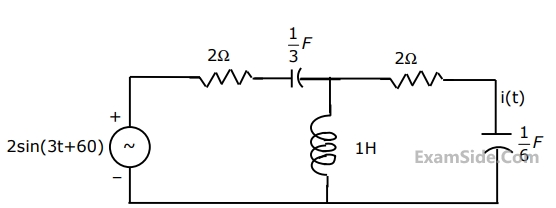
Determine the current, i(t), in the circuit given below, (Fig.), using the Thevenin's theorem.