For the amplifier of given figure,
$${I_C}\, = \,1.3\,mA,\,{R_C}\, = \,2\,k\Omega ,\,{R_E}\, = \,500\,\Omega ,$$
$${V_T}\, = \,26\,mV,\,\beta \, = \,100,\,{V_{CC}}\, = \,15V,$$
$${V_s}\, = \,0.01\,\sin \left( {\omega t} \right)\,V\,and\,{C_b}\, = \,{C_C}\, = \,10\,\mu F.$$

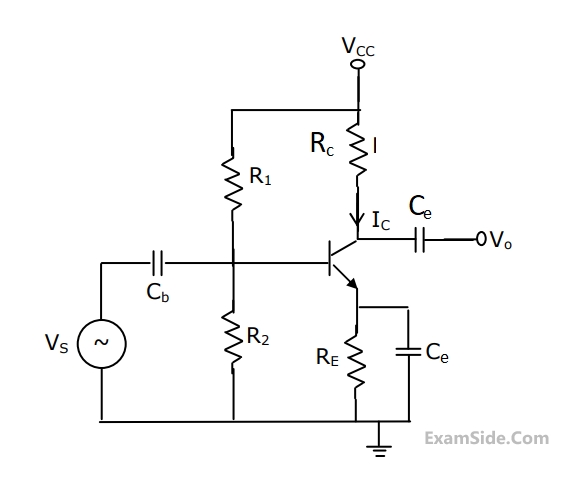
(a)What is the small-signal voltage gain, $${A_V} = {V_0}/{V_s}?$$
(b)What is the approximate $${A_{v,}}\,\,if\,\,{C_e}\,\,$$ is removed?
(c)What will $${V_0}\,be\,if\,{C_b}$$ is short circuited?

A bipolar junction transistor amplifier circuit is shown in the figure. Assume that the current source I_bias is ideal, and the transistor has very large$$\beta ,\,\,{r_{b\,\,}} = \,\,0,$$ and the $${r_0}\, \to \,\infty $$.

Determine the ac small-signal mid-band and voltage gain $$\left( {{V_o}/{V_s}} \right),$$ input resistance (R₁, and output resistance (R₀) of the circuit. Assume $${V_{T\,\,}} = \,\,26\,mV.$$

In the circuit of fig. Determine the resistance R_o seen by the output terminals, ignore the effects of R₁ and R₂.

The transistor in the circuit shown in the figure. is so biased (dc biasing N/W is not shown) that the dc collector current I_C = 1mA. Supply is V_CC = 5V.

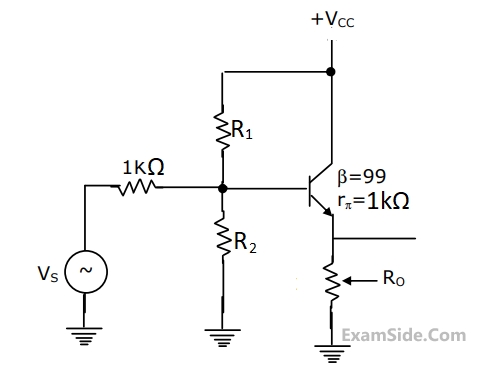
The N/W components have following values, R_C = 2$$k\Omega $$,
R_S = $$1.4k\Omega $$,
R_E = $$100\Omega $$.

The transistor has specifications, $$\beta \,\, = \,\,100$$
and base spreading resistance $${r_{bb\,}}^1\, = \,100\Omega $$

$$Assume\,\,{{KT} \over q}\,\, = \,\,25\,mV$$

Evaluate input resistance R_i for two cases. At a frequency of 10 kHz

(a)C_E, the bypass capacitor across R_E is 25 $$\mu F$$
(b)The bypass capacitor C_E is removed leaving R_E unbypassed.