ExamSIDE (Powered by ExamGOAL)
Questions
PREVIOUS NEXT
1
GATE ECE 2015 Set 3
MCQ (Single Correct Answer)
+2
-0.6
A realization of a stable discrete time system is shown in the figure. If the system is excited by a unit step sequence input x[n ] , the response y[ n] is GATE ECE 2015 Set 3 Signals and Systems - Discrete Time Signal Z Transform Question 18 English
A
$$4{\left( { - {1 \over 3}} \right)^n}u\left[ n \right] - 5{\left( { - {2 \over 3}} \right)^n}u\left[ n \right]$$
B
$$5{\left( { - {2 \over 3}} \right)^n}u\left[ n \right] - 3{\left( { - {1 \over 3}} \right)^n}u\left[ n \right]$$
C
$$5{\left( {{1 \over 3}} \right)^n}u\left[ n \right] - 5{\left( {{2 \over 3}} \right)^n}u\left[ n \right]$$
D
$$5{\left( {{2 \over 3}} \right)^n}u\left[ n \right] - 5{\left( {{1 \over 3}} \right)^n}u\left[ n \right]$$
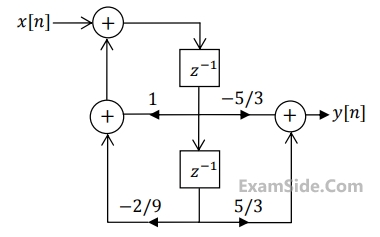
2
GATE ECE 2015 Set 3
MCQ (Single Correct Answer)
+2
-0.6
Suppose x $$\left[ n \right]$$ is an absolutely summable discrete-time signal. Its z-transform is a rational function with two poles and two zeroes. The poles are at z = ± 2j. Which one of the following statements is TRUE for the signal x=$$\left[ n \right]$$ ?
A
It is a finite duration signal.
B
It is a causal signal.
C
It is a non-causal signal.
D
It is a periodic signal.
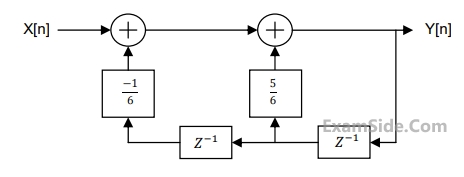
3
GATE ECE 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
The pole-zero diagram of a causal and stable discrete-time system is shown in the figure. The zero at the origin has multiplicity 4. The impulse response of the system is ℎ[n]. If ℎ[0] =1, we can conclude. GATE ECE 2015 Set 1 Signals and Systems - Discrete Time Signal Z Transform Question 20 English
A
h (n) is real for all n.
B
h (n) is purely imaginary for all n.
C
h (n) is real for only even n.
D
h (n) is purely imaginary for only odd n ݊
4
GATE ECE 2015 Set 1
MCQ (Single Correct Answer)
+2
-0.6
For the discrete-time system shown in the figure, the poles of the system transfer function are located at GATE ECE 2015 Set 1 Signals and Systems - Discrete Time Signal Z Transform Question 19 English
A
2, 3
B
1/2, 3
C
1/2 , 1/3
D
2, 1/3
PREVIOUS NEXT
GATE ECE Subjects
Network Theory
State Equations For Networks Network Elements Network Theorems Two Port Networks Transient Response Sinusoidal Steady State Response Network Graphs Miscellaneous
Control Systems
Basic of Control Systems Signal Flow Graph and Block Diagram Time Response Analysis Stability Root Locus Diagram Frequency Response Analysis Compensators State Space Analysis
Electronic Devices and VLSI
PN Junction Semiconductor Physics IC Basics and MOSFET BJT and FET
Analog Circuits
Diodes Bipolar Junction Transistor Frequency Response FET and MOSFET Oscillators Operational Amplifier Feedback Amplifier Power Amplifier 555 Timer
Digital Circuits
Number System and Code Convertions Boolean Algebra Logic Gates Combinational Circuits Sequential Circuits Semiconductor Memories Logic Families Analog to Digital and Digital to Analog Converters
Microprocessors
Instruction Set and Programming with 8085 Pin Details of 8085 and Interfacing with 8085
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Communications
Fundamentals of Information Theory Noise In Digital Communication Analog Communication Systems Digital Communication Systems Random Signals and Noise
Electromagnetics
Maxwell Equations Transmission Lines Uniform Plane Waves Waveguides Antennas Miscellaneous
General Aptitude
Numerical Ability Verbal Ability
Engineering Mathematics
Linear Algebra Calculus Vector Calculus Complex Variable Probability and Statistics Differential Equations Numerical Methods Transform Theory
EXAM MAP
Joint Entrance Examination
JEE MainJEE AdvancedWB JEEBITSATMHT CETKCETCOMEDKVITEEE
Medical
NEET
Graduate Aptitude Test in Engineering
GATE CSEGATE ECEGATE EEGATE MEGATE CEGATE PIGATE IN
CBSE
Class 12