A product made in two factories $$P$$ and $$Q,$$ is transported to two destinations, $$R$$ and $$S.$$ The per unit costs of transportation (in Rupees) from factories to destinations are as per the following matrix.

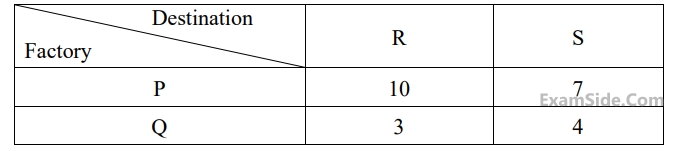
Factory $$P$$ produces $$7$$ units and factory $$Q$$ produces $$9$$ units of the product. Each destination requires $$8$$ units. If the north-west corner method provides the total transportation cost as $$X$$ (in Rupees) and the optimized (the minimum) total transportation cost $$Y$$ (in Rupees), then $$(X$$-$$Y),$$ in Rupees, is

For the standard transportation linear programme with $$m$$ sources and $$n$$ destinations and total supply equaling total demand, an optimal solution (lowest cost) with the smallest number of non-zero $${X_{ij}}$$ values (amounts from source $$i$$ to destination $$j$$) is desired. The best upper bound for this number is

A company has two factories $${S_1},$$ $${S_2}$$ and two warehouses $${D_1},$$ $${D_2}$$ . the supplies from $${S_1}$$ and $${S_2}$$ are $$50$$ and $$40$$ units respectively. Warehouse $${D_1},$$ requires a minimum of $$20$$ units and a maximum of $$40$$ units. Warehouse $${D_2},$$ requires a minimum of $$20$$ units and, over and above, it can take as much as can be supplied. A balanced transport-ation problem is to be formulated for the above situation. The number of supply points, the number of demand points, and the total supply (or total demand) in the balanced transportation problem respectively are

The supply at three sources is $$50, 40$$ and $$60$$ units respectively whilst the demand at the four destinations is $$20, 30, 10$$ and $$50$$ units. In solving this transportation problem