For a polynomial g(x) with real coefficients, let m_g denote the number of distinct real roots of g(x). Suppose S is the set of polynomials with real coefficients defined by

$$S = \{ {({x^2} - 1)^2}({a_0} + {a_1}x + {a_2}{x^2} + {a_3}{x^3}):{a_0},{a_1},{a_2},{a_3} \in R\} $$;

For a polynomial f, let f' and f'' denote its first and second order derivatives, respectively. Then the minimum possible value of (m_f' + m_f''), where f $$ \in $$ S, is ..............

let e denote the base of the natural logarithm. The value of the real number a for which the right hand limit

$$\mathop {\lim }\limits_{x \to {0^ + }} {{{{(1 - x)}^{1/x}} - {e^{ - 1}}} \over {{x^a}}}$$

is equal to a non-zero real number, is .............

A small roller of diameter 20 cm has an axle of diameter 10 cm (see figure below on the left). It is on a horizontal floor and a meter scale is positioned horizontally on its axle with one edge of the scale on top of the axle (see figure on the right). The scale is now pushed slowly on the axle so that it moves without slipping on the axle, and the roller starts rolling without slipping. After the roller has moved 50 cm, the position of the scale will look like (figures are schematic and not drawn to scale)

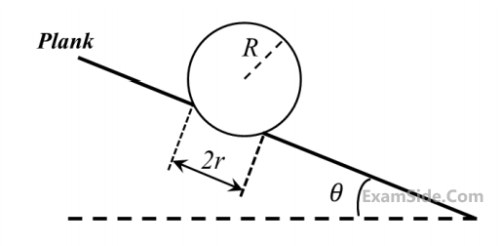
A football of radius R is kept on a hole of radius r (r < R) made on a plank kept horizontally. One end of the plank is now lifted so that it gets tilted making an angle $$\theta $$ from the horizontal as shown in the figure below. The maximum value of $$\theta $$ so that the football does not start rolling down the plank satisfies (figure is schematic and not drawn to scale)