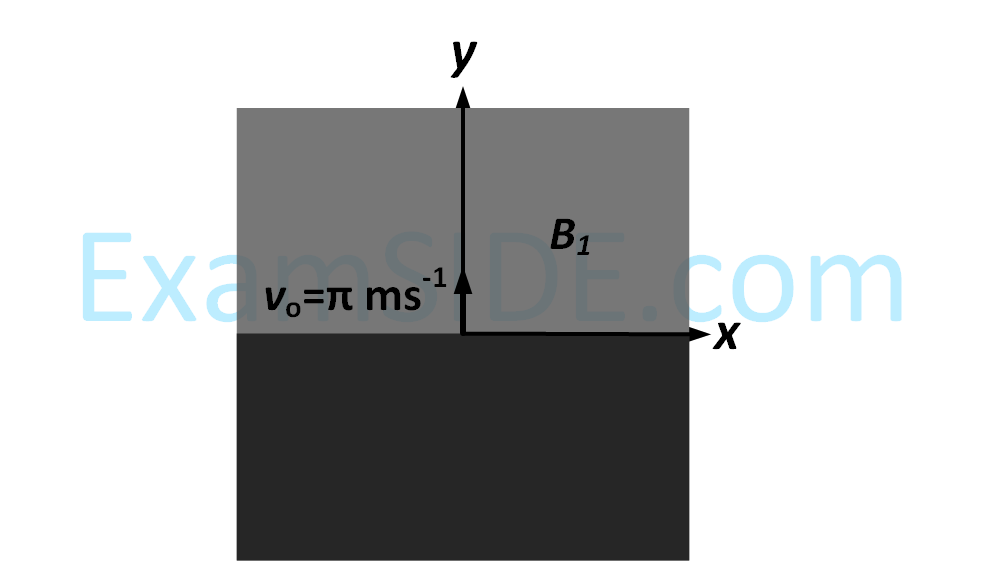
In the $$xy$$-plane, the region $$y > 0$$ has a uniform magnetic field $${B_1}\widehat k$$ and the region $$y < 0$$ has another uniform magnetic field $${B_2}\widehat k.$$ A positively charged particle is projected from the origin along the positive $$y$$-axis with speed $${v_0} = \pi \,m{s^{ - 1}}$$ at $$t=0,$$ as shown in the figure. Neglect gravity in this problem. Let $$t=T$$ be the time when the particle crosses the $$x$$-axis from below for the first time. If $${B_2} = 4{B_1},$$ the average speed of the particle, in $$m{s^{ - 1}},$$ along the $$x$$-axis in the time interval $$T$$ is ___________.

Two conducting cylinders of equal length but different radii are connected in series between two heat baths kept at temperatures $${T_1} = 300\,K$$ and $${T_2} = 100\,K$$, as shown in the figure. The radius of the bigger cylinder is twice that of the smaller once and the thermal conductivities of the materials of the smaller and the larger cylinders are $${K_1}$$ and $${K_2}$$ respectively. If the temperature at the junction of the two cylinders in the steady state is $$200$$ $$K,$$ then $${K_1}/{K_2} = $$ ______________.

Sunlight of intensity $$1.3$$ $$kW\,{m^{ - 2}}$$ is incident normally on a thin convex lens of focal length $$20$$ cm. Ignore the energy loss of light due to the lens and assume that the lens aperture size is much smaller than its focal length. The average intensity of light, in $$kW\,{m^{ - 2}},$$ at a distance $$22$$ cm from the lens on the other side is ___________.

In electromagnetic theory, the electric and magnetic phenomena are related to each other. Therefore, the dimensions of electric and magnetic quantities must also be related to each other. In the questions below, $$[E]$$ and $$[B]$$ stand for dimensions of electric and magnetic fields respectively, while $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ stand for dimensions of the permittivity and permeability of free space respectively. $$\left[ L \right]$$ and $$\left[ T \right]$$ are dimensions of length and time respectively. All the quantities are given in $$SI$$ units.

The relation between $$\left[ {{\varepsilon _0}} \right]$$ and $$\left[ {{\mu _0}} \right]$$ is