1
JEE Advanced 2016 Paper 2 Offline
MCQ (More than One Correct Answer)
+4
-2

In the circuit shown below, the key is pressed at time t = 0. Which of the following statement(s) is (are) true?
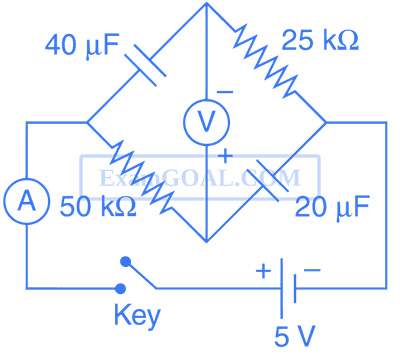

2
JEE Advanced 2016 Paper 2 Offline
MCQ (More than One Correct Answer)
+4
-2

Light of wavelength $$\lambda$$ph falls on a cathode plate inside a vacuum tube as shown in the figure. The work function of the cathode surface is $$\phi$$ and the anode is a wire mesh of conducting material kept at a distance d from the cathode. A potential difference V is maintained between the electrodes. If the minimum de-Broglie wavelength of the electrons passing through the anode is $$\lambda$$e, which of the following statement(s) is (are) true?


3
JEE Advanced 2016 Paper 2 Offline
MCQ (Single Correct Answer)
+3
-0

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $$\omega$$ is an example of a non-inertial frame of reference. The relationship between the force $$\overrightarrow F $$rot experienced by a particle of mass m moving on the rotating disc and the force $$\overrightarrow F $$in experienced by the particle in an inertial frame of reference is,
$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The distance r of the block at time t is
$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The distance r of the block at time t is
4
JEE Advanced 2016 Paper 2 Offline
MCQ (Single Correct Answer)
+3
-0

A frame of the reference that is accelerated with respect to an inertial frame of reference is called a non-inertial frame of reference. A coordinate system fixed on a circular disc rotating about a fixed axis with a constant angular velocity $$\omega$$ is an example of a non-inertial frame of reference. The relationship between the force $$\overrightarrow F $$rot experienced by a particle of mass m moving on the rotating disc and the force $$\overrightarrow F $$in experienced by the particle in an inertial frame of reference is,
$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The net reaction of the disc on the block is
$$\overrightarrow F $$rot = $$\overrightarrow F $$in + 2m ($$\overrightarrow v $$rot $$\times$$ $$\overrightarrow \omega $$) + m ($$\overrightarrow \omega $$ $$\times$$ $$\overrightarrow r $$) $$\times$$ $$\overrightarrow \omega $$,
where, vrot is the velocity of the particle in the rotating frame of reference and r is the position vector of the particle with respect to the centre of the disc.

Now, consider a smooth slot along a diameter of a disc of radius R rotating counter-clockwise with a constant angular speed $$\omega$$ about its vertical axis through its centre. We assign a coordinate system with the origin at the centre of the disc, the X-axis along the slot, the Y-axis perpendicular to the slot and the Z-axis along the rotation axis ($$\omega$$ = $$\omega$$ $$\widehat k$$). A small block of mass m is gently placed in the slot at r = (R/2)$$\widehat i$$ at t = 0 and is constrained to move only along the slot.
The net reaction of the disc on the block is
Paper analysis
Total Questions
Chemistry
18
Mathematics
18
Physics
18
More papers of JEE Advanced
JEE Advanced 2025 Paper 2 Online
JEE Advanced 2025 Paper 1 Online
JEE Advanced 2024 Paper 2 Online
JEE Advanced 2024 Paper 1 Online
JEE Advanced 2023 Paper 2 Online
JEE Advanced 2023 Paper 1 Online
JEE Advanced 2022 Paper 2 Online
JEE Advanced 2022 Paper 1 Online
JEE Advanced 2021 Paper 2 Online
JEE Advanced 2021 Paper 1 Online
JEE Advanced 2020 Paper 2 Offline
JEE Advanced 2020 Paper 1 Offline
JEE Advanced 2019 Paper 2 Offline
JEE Advanced 2019 Paper 1 Offline
JEE Advanced 2018 Paper 2 Offline
JEE Advanced 2018 Paper 1 Offline
JEE Advanced 2017 Paper 2 Offline
JEE Advanced 2017 Paper 1 Offline
JEE Advanced 2016 Paper 2 Offline
JEE Advanced 2016 Paper 1 Offline
JEE Advanced 2015 Paper 2 Offline
JEE Advanced 2015 Paper 1 Offline
JEE Advanced 2014 Paper 2 Offline
JEE Advanced 2014 Paper 1 Offline
JEE Advanced 2013 Paper 2 Offline
JEE Advanced 2013 Paper 1 Offline
IIT-JEE 2012 Paper 2 Offline
IIT-JEE 2012 Paper 1 Offline
IIT-JEE 2011 Paper 1 Offline
IIT-JEE 2011 Paper 2 Offline
IIT-JEE 2010 Paper 2 Offline
IIT-JEE 2010 Paper 1 Offline
IIT-JEE 2009 Paper 2 Offline
IIT-JEE 2009 Paper 1 Offline
IIT-JEE 2008 Paper 2 Offline
IIT-JEE 2008 Paper 1 Offline
IIT-JEE 2007
IIT-JEE 2007 Paper 2 Offline
IIT-JEE 2006
IIT-JEE 2006 Screening
IIT-JEE 2005 Screening
IIT-JEE 2005
IIT-JEE 2004
IIT-JEE 2004 Screening
IIT-JEE 2003
IIT-JEE 2003 Screening
IIT-JEE 2002
IIT-JEE 2002 Screening
IIT-JEE 2001
IIT-JEE 2001 Screening
IIT-JEE 2000 Screening
IIT-JEE 2000
IIT-JEE 1999 Screening
IIT-JEE 1999
IIT-JEE 1998
IIT-JEE 1998 Screening
IIT-JEE 1997
IIT-JEE 1996
IIT-JEE 1995 Screening
IIT-JEE 1995
IIT-JEE 1994
IIT-JEE 1993
IIT-JEE 1992
IIT-JEE 1991
IIT-JEE 1990
IIT-JEE 1989
IIT-JEE 1988
IIT-JEE 1987
IIT-JEE 1986
IIT-JEE 1985
IIT-JEE 1984
IIT-JEE 1983
IIT-JEE 1982
IIT-JEE 1981
IIT-JEE 1980
IIT-JEE 1979
IIT-JEE 1978
JEE Advanced
Papers
2020
2019
2018
2017
2016
1997
1996
1994
1993
1992
1991
1990
1989
1988
1987
1986
1985
1984
1983
1982
1981
1980
1979
1978