Let $$F:R \to R$$ be a thrice differentiable function. Suppose that
$$F\left( 1 \right) = 0,F\left( 3 \right) = - 4$$ and $$F'\left( x \right) < 0$$ for all $$x \in \left( {{1 \over 2},3} \right).$$ Let $$f\left( x \right) = xF\left( x \right)$$ for all $$x \in R.$$

The correct statement(s) is (are)

If $$\alpha = \int\limits_0^1 {\left( {{e^{9x + 3{{\tan }^{ - 1}}x}}} \right)\left( {{{12 + 9{x^2}} \over {1 + {x^2}}}} \right)} dx$$ where $${\tan ^{ - 1}}x$$ takes only principal values, then the value of $$\left( {{{\log }_e}\left| {1 + \alpha } \right| - {{3\pi } \over 4}} \right)$$ is

Let m and n be two positive integers greater than 1. If $$$\mathop {\lim }\limits_{\alpha \to 0} \left( {{{{e^{\cos \left( {{\alpha ^n}} \right)}} - e} \over {{\alpha ^m}}}} \right) = - \left( {{e \over 2}} \right)$$$ then the value of $${m \over n}$$ is _________.

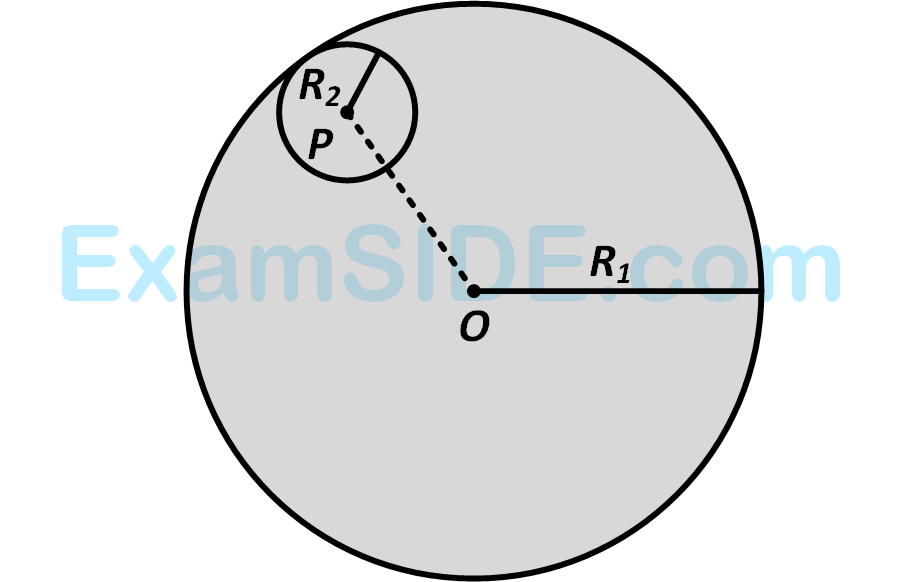
Consider a uniform spherical charge distribution of radius $${R_1}$$ centred at the origin $$O.$$ In this distribution, a spherical cavity of radius $${R_2},$$ centred at $$P$$ with distance $$OP=a$$ $$ = {R_1} - {R_2}$$ (see figure) is made. If the electric field inside the cavity at position $$\overrightarrow r $$ is $$\overrightarrow E \overrightarrow {\left( r \right)} ,$$ then the correct statement(s) is (are)