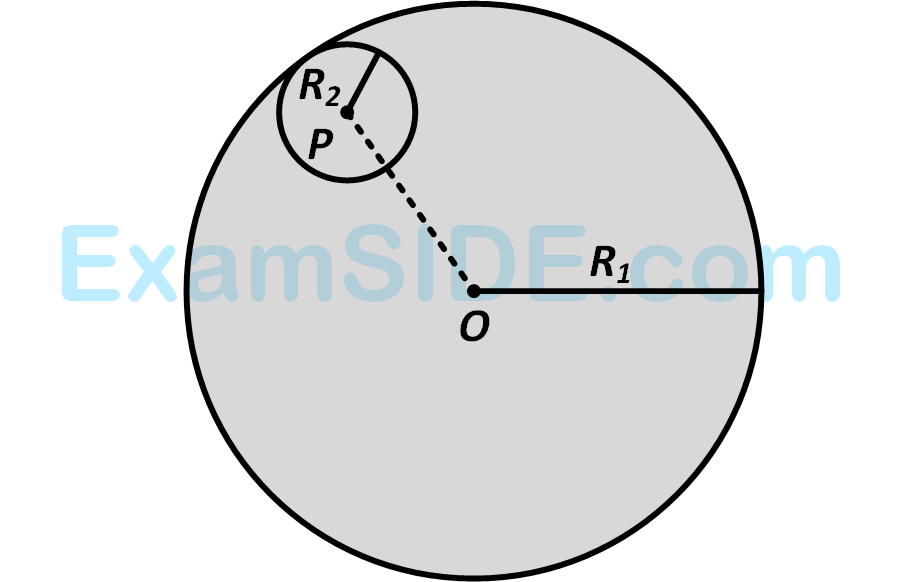
Consider a uniform spherical charge distribution of radius $${R_1}$$ centred at the origin $$O.$$ In this distribution, a spherical cavity of radius $${R_2},$$ centred at $$P$$ with distance $$OP=a$$ $$ = {R_1} - {R_2}$$ (see figure) is made. If the electric field inside the cavity at position $$\overrightarrow r $$ is $$\overrightarrow E \overrightarrow {\left( r \right)} ,$$ then the correct statement(s) is (are)

A spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r) is the pressure at r (r < R), then the correct option(s) is(are)

The densities of two solid spheres A and B of the same radii R vary with radial distance r as $${\rho _A}(r) = k\left( {{r \over R}} \right)$$ and $${\rho _B}(r) = k{\left( {{r \over R}} \right)^5}$$, , respectively, where k is a constant. The moments of inertia of the individual spheres about axes passing through their centres are $${I_A}$$ and $${I_B}$$, respectively. If, $${{{I_B}} \over {{I_A}}} = {n \over {10}}$$, the value of n is

The energy of a system as a function of time t is given as E(t) = $${A^2}\exp \left( { - \alpha t} \right)$$, where $$\alpha = 0.2\,{s^{ - 1}}$$. The measurement of A has an error of 1.25 %. If the error in the measurement of time is 1.50 %, the percentage error in the value of E(t) at t = 5 s is