Four identical thin, square metal sheets, $S_1, S_2, S_3$ and $S_4$, each of side $a$ are kept parallel to each other with equal distance $d(\ll a)$ between them, as shown in the figure. Let $${C_0} = {{{\varepsilon _0}{a^2}} \over d}$$, where $\varepsilon_0$ is the permittivity of free space.

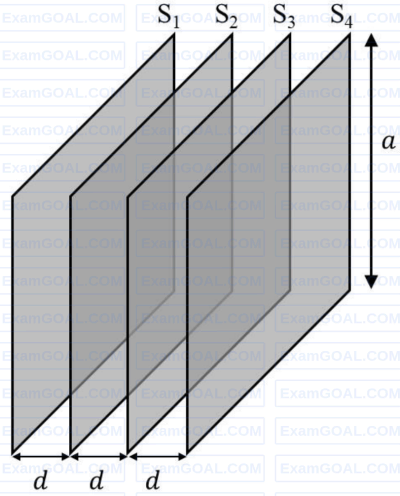
Match the quantities mentioned in List-I with their values in List-II and choose the correct option.

List-I	List-II
(P) The capacitance between $S_1$ and $S_4$, with $S_2$ and $S_3$ not connected, is	(1) $3C_0$
(Q) The capacitance between $S_1$ and $S_4$, with $S_2$ shorted to $S_3$, is	(2) $\frac{C_0}{2}$
(R) The capacitance between $S_1$ and $S_3$, with $S_2$ shorted to $S_4$, is	(3) $\frac{C_0}{3}$
(S) The capacitance between $S_1$ and $S_2$, with $S_3$ shorted to $S_1$, and $S_2$ shorted to $S_4$, is	(4) $\frac{2C_0}{3}$
	(5) $2C_0$

A container has a base of $50 \mathrm{~cm} \times 5 \mathrm{~cm}$ and height $50 \mathrm{~cm}$, as shown in the figure. It has two parallel electrically conducting walls each of area $50 \mathrm{~cm} \times 50 \mathrm{~cm}$. The remaining walls of the container are thin and non-conducting. The container is being filled with a liquid of dielectric constant 3 at a uniform rate of $250 \mathrm{~cm}^3 \mathrm{~s}^{-1}$. What is the value of the capacitance of the container after 10 seconds?

[Given: Permittivity of free space $\epsilon_0=9 \times 10^{-12} \mathrm{C}^2 \mathrm{~N}^{-1} \mathrm{~m}^{-2}$, the effects of the non-conducting walls on the capacitance are negligible]

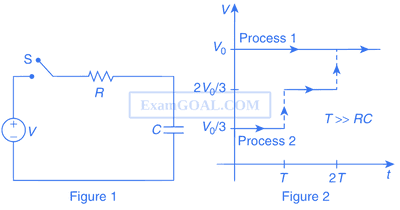
Consider a simple RC circuit as shown in Figure 1.

Process 1 : In the circuit the switch S is closed at t = 0 and the capacitor is fully charged to voltage V₀ (i.e. charging continues for time T >> RC). In the process some dissipation (E_D) occurs across the resistance R. The amount of energy finally stored in the fully charged capacitor is E_C.

Process 2 : In a different process the voltage is first set to $${{{V_0}} \over 3}$$ and maintained for a charging time T >> RC. Then, the voltage is raised to $${{2{V_0}} \over 3}$$ without discharging the capacitor and again maintained for a time T >> RC. The process is repeated one more time by raising the voltage to V₀ and the capacitor is charged to the same final voltage V₀ as in Process 1.

These two processes are depicted in Figure 2.

In Process 1, the energy stored in the capacitor E_C and heat dissipated across resistance E_D are related by

Consider a simple RC circuit as shown in Figure 1.

Process 1 : In the circuit the switch S is closed at t = 0 and the capacitor is fully charged to voltage V₀ (i.e. charging continues for time T >> RC). In the process some dissipation (E_D) occurs across the resistance R. The amount of energy finally stored in the fully charged capacitor is E_C.

Process 2 : In a different process the voltage is first set to $${{{V_0}} \over 3}$$ and maintained for a charging time T >> RC. Then, the voltage is raised to $${{2{V_0}} \over 3}$$ without discharging the capacitor and again maintained for a time T >> RC. The process is repeated one more time by raising the voltage to V₀ and the capacitor is charged to the same final voltage V₀ as in Process 1.

These two processes are depicted in Figure 2.

In Process 2, total energy dissipated across the resistance E_D is