1
JEE Advanced 2018 Paper 1 Offline
Numerical
+3
-0

A ring and disc are initially at rest, side by side, at the top of an inclined plane which makes an angle $${60^ \circ }$$ with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is $$\left( {2 - \sqrt 3 } \right)/\sqrt {10} \,\,s,$$ then the height of the top of the inclined plane, in metres is ______________ . Take $$g = 10\,\,m{s^{ - 2}}.$$
Your input ____
2
JEE Advanced 2015 Paper 2 Offline
Numerical
+4
-0
The densities of two solid spheres A and B of the same radii R vary with radial distance r as $${\rho _A}(r) = k\left( {{r \over R}} \right)$$ and $${\rho _B}(r) = k{\left( {{r \over R}} \right)^5}$$, , respectively, where k is a constant. The moments of inertia of the individual spheres about axes passing through their centres are $${I_A}$$ and $${I_B}$$, respectively. If, $${{{I_B}} \over {{I_A}}} = {n \over {10}}$$, the value of n is
Your input ____
3
JEE Advanced 2015 Paper 1 Offline
Numerical
+4
-0
Two identical uniform discs roll without slipping on two different surfaces AB and CD (see figure) starting at A and C with linear speeds v1 and v2, respectively, and always remain in contact with the surfaces. If they reach B and D with the same linear speed and v1 = 3 m/s, then v2 in m/s is (g = 10 m/s2)
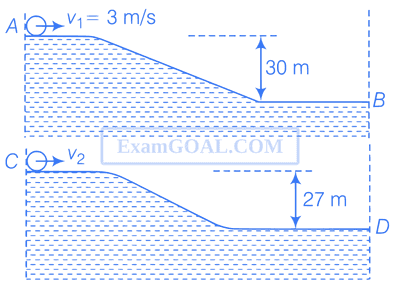

Your input ____
4
JEE Advanced 2014 Paper 1 Offline
Numerical
+3
-0
A uniform circular disc of mass 1.5 kg and radius 0.5 m is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude F = 0.5 N are applied simultaneously along the three sides of an equilateral triangle XYZ with its vertices on the perimeter of the disc (see figure). One second after applying the forces, the angular speed of the disc in rad s-1 is


Your input ____
Questions Asked from Rotational Motion (Numerical)
Number in Brackets after Paper Indicates No. of Questions
JEE Advanced 2024 Paper 1 Online (2)
JEE Advanced 2023 Paper 2 Online (1)
JEE Advanced 2023 Paper 1 Online (1)
JEE Advanced 2022 Paper 1 Online (2)
JEE Advanced 2021 Paper 1 Online (1)
JEE Advanced 2018 Paper 1 Offline (2)
JEE Advanced 2015 Paper 2 Offline (1)
JEE Advanced 2015 Paper 1 Offline (1)
JEE Advanced 2014 Paper 1 Offline (2)
JEE Advanced 2013 Paper 1 Offline (1)
IIT-JEE 2011 Paper 1 Offline (2)
JEE Advanced Subjects
Physics
Mechanics
Units & Measurements Motion Laws of Motion Work Power & Energy Impulse & Momentum Rotational Motion Properties of Matter Heat and Thermodynamics Simple Harmonic Motion Waves Gravitation
Electricity
Electrostatics Current Electricity Capacitor Magnetism Electromagnetic Induction Alternating Current Electromagnetic Waves
Optics
Modern Physics
Chemistry
Physical Chemistry
Some Basic Concepts of Chemistry Structure of Atom Redox Reactions Gaseous State Chemical Equilibrium Ionic Equilibrium Solutions Thermodynamics Chemical Kinetics and Nuclear Chemistry Electrochemistry Solid State Surface Chemistry
Inorganic Chemistry
Periodic Table & Periodicity Chemical Bonding & Molecular Structure Isolation of Elements Hydrogen s-Block Elements p-Block Elements d and f Block Elements Coordination Compounds Salt Analysis
Organic Chemistry
Mathematics
Algebra
Quadratic Equation and Inequalities Sequences and Series Mathematical Induction and Binomial Theorem Matrices and Determinants Permutations and Combinations Probability Vector Algebra 3D Geometry Statistics Complex Numbers
Trigonometry
Coordinate Geometry
Calculus