The system under consideration is an RC low -pass filter (RC-LPF) with R = 1.0 $$k\Omega $$ and C = 1.0 $$\mu F$$.

Let $${t_g}$$ (f) be the group delay function of the given RC-LPF and $${f_2}$$ = 100 Hz. Then $${t_g}$$$${(f_2)}$$ in ms, is

In Fig. m(t) = $$ = {{2\sin 2\pi t} \over t}$$, $$s(t) = \cos \,200\pi t\,\,andn(t) = {{\sin 199\pi t} \over t}$$.

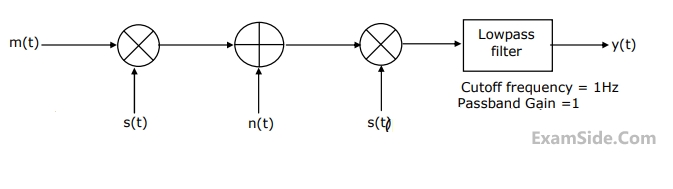
The output y(t) will be

A system has a phase response given by $$\phi \,(\omega )$$ where $$\omega $$ is the angular frequency. The phase delay and group delay at $$\omega $$ = $${\omega _0}$$ are respectively given by

The input to a matched filter is given by $$s(t) = \left\{ {\matrix{ {10\sin (2\pi \times {{10}^6}t),} & {0 < \left| t \right| < {{10}^{ - 4}}\sec } \cr 0 & {Otherwise} \cr } } \right.$$

The peak amplitude of the filter output is