For the circuit in Fig. Which is in steady state,

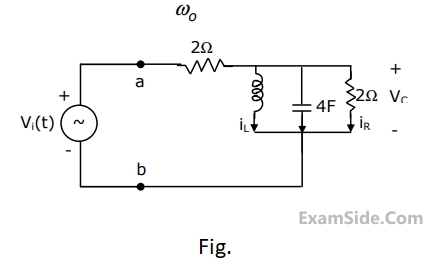
(a)Find the frequency $${\omega _0}$$ at which the magnitude of the impedance across terminals a, b reaches maximum.

(b) Find the impedance across a, b at the frequency $${\omega _0}$$.

(c) If $${v_i}\left( t \right) = V\,\,\sin \left( {{\omega _0}t} \right),$$ find $${i_L}\left( t \right),\,\,{i_c}\left( t \right),{i_R}\left( t \right).$$

A coil with a quality factor $$(Q)$$ of $$10$$ is put in series with a capacitor $${C_1}$$ of $$10\,\,\mu F,$$ and the combination is found to draw maximum current when a sinusoidal voltage of frequency $$50$$ $$Hz$$ is applied. A second capacitor $${C_2}$$ is now in parallel with the circuit. What should be the capacitance of $${C_2}$$ for combined circuit to act purely as a resistance for a sinusoidal excitation at a frequency of $$100$$ $$Hz$$? Calculate the rms current drawn by the combined circuit at $$100$$ $$Hz$$ if the applied voltage is $$100V$$ (rms).

Determine the frequency of resonance and the resonant impedance of the parallel circuit shown in figure. What happens when $$L = C{R^2}$$?

In the circuit of Fig., all currents and voltage are sinusoids of frequency $$\omega $$ rad/sec.

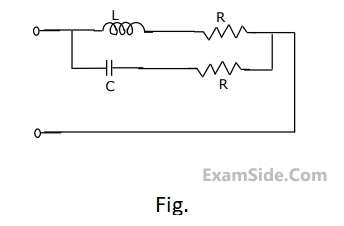
(a) Find the impedance to the right of $$\left( {A,\,\,\,\,\,\,B} \right)$$ at $$\omega \,\,\, = \,\,\,\,0$$ rad/sec and $$\omega \,\,\, = \,\,\,\,\infty $$ rad/sec.

(b) If $$\omega \,\,\, = \,\,\,\,{\omega _0}$$ rad/sec and $${i_1}\left( t \right) = \,\,{\rm I}\,\,\,\sin \,\left( {{\omega _0}t} \right)\,{\rm A},$$ where $${\rm I}$$ is positive, $${{\omega _0}\,\, \ne \,\,0}$$, $${{\omega _0}\,\, \ne \,\,\infty }$$, then find $${\rm I}$$, $${{\omega _0}}$$ and $${i_2}\left( t \right)$$