1
GATE ECE 2001
Subjective
+5
-0
The Fourier transform $$G(\omega )$$ of the signal g(t) in Fig.(1) is given as
$$G(\omega ) = {1 \over {{\omega ^2}}}({e^{j\omega }} - j\omega {e^{j\omega }} - 1)$$.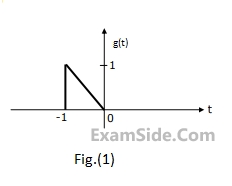
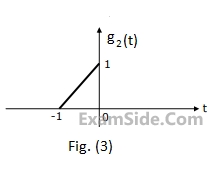
$$G(\omega ) = {1 \over {{\omega ^2}}}({e^{j\omega }} - j\omega {e^{j\omega }} - 1)$$.
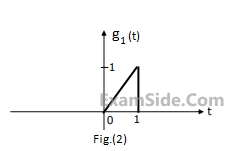
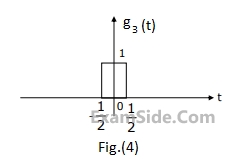
Using this information, and the time-shifting and time-scaling properties, determine and Fourier transform of signals in Fig (2), (3) and (4).


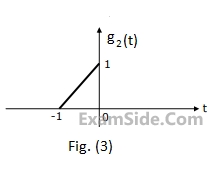

2
GATE ECE 1998
Subjective
+5
-0
Consider a rectangular pulse g(t) existing between $$t = \, - {T \over 2}\,and\,{T \over 2}$$. Find and sketch the pulse obtained by convolving g(t) with itself. The Fourier transform of g(t) is a sinc function. Write down the Fourier transform of the pulse obtained by the above convolution.
3
GATE ECE 1995
Subjective
+5
-0
A signal v(t)= [1+ m(t) ] cos $$({\omega _c}t)$$ is detected using a square law detector, having the characteristic $${v_0}(t) = {v^2}(t)$$. If the Fourier transform of m(t) is constant, $${M_0}$$, extending from - $${f_{m\,}}\,to\, + {f_{m\,}}$$, sketch the Fourier transform of $${v_0}(t)$$ in the frequency range-$${f_{m\,}}\, < f < {f_{m\,}}$$.
Questions Asked from Fourier Transform (Marks 5)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics