In Fig. 1, a linear time invariant discrete system is shown. Blocks labeled D represent unit delay elements. For $$n\, < 0,$$ you may assume that $$x\left( n \right),$$ $${y_1}\left( n \right),\,\,{y_2}\left( n \right)$$ are all zero.

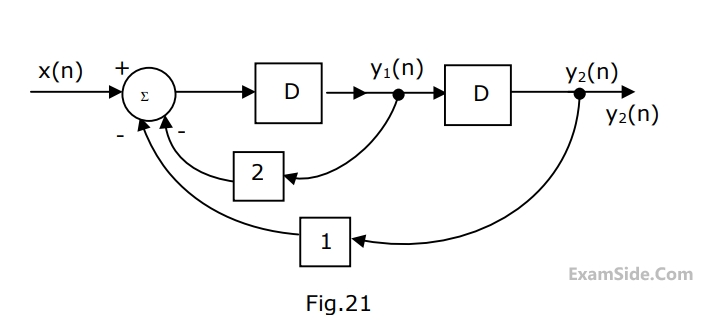
(a) Find the expression for $${y_1}\left( n \right)$$ and $${y_2}\left( n \right)$$ in terms of $$x\left( n \right).$$
(b) Find the transfer function $${y_2}\left( z \right)/X\left( z \right)$$ in the $$z$$-domain.
(c) If $$x\left( n \right) = 1$$ at $$n = 0$$ or $$x\left( n \right) = 0$$ otherwise

Find $${y_2}\left( n \right).$$

A system having a unit impulse response $$h\left( n \right)$$ = $$u\left( n \right)$$ is excited by a signal $$x\left( n \right)$$ $$ = \,{\alpha ^n}\,\,u\left( n \right).\,$$ Determine the output $$y\left( n \right)$$

In the linear time-invariant system shown in Fig. 1, blocks labeled D represent unit delay elements. Find the expression for $$y\left( n \right),$$ and also the transfer function $${{Y\left( z \right)} \over {X\left( z \right)}}$$ in the $$z$$-domain.