1
GATE ECE 2000
Subjective
+5
-0
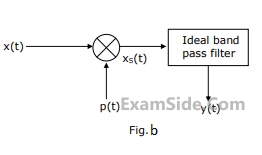
A band limited signal x(t) with a spectrum X(f) as shown in Fig. a is processed as shown in Fig.b. p(t) is a periodic train of impulses as in Fig. c. The ideal band pass filter has a pass band from 26 KHz to 34 KHz.
(a) Calculate the Fourier series coefficients $${c_n}$$ in the Fourier expansion of p(t) in form $$p(t) = \sum\limits_{n = - \infty }^{ + \infty } {{c_n}} \,\exp \,\,(j\,n\,2\pi \,t/T)$$.
(b) Find the Fourier Transform of p(t).
(c) Obtain and sketch the spectrum of $${x_s}(t)$$.
(d) Obtain and sketch the spectrum of y(t).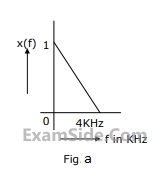

(a) Calculate the Fourier series coefficients $${c_n}$$ in the Fourier expansion of p(t) in form $$p(t) = \sum\limits_{n = - \infty }^{ + \infty } {{c_n}} \,\exp \,\,(j\,n\,2\pi \,t/T)$$.
(b) Find the Fourier Transform of p(t).
(c) Obtain and sketch the spectrum of $${x_s}(t)$$.
(d) Obtain and sketch the spectrum of y(t).



2
GATE ECE 1993
Subjective
+5
-0
A low pass signal m(t) band-limited to B Hz is sampled by a periodic rectangular pulse train, $${p_\tau }(t)$$ of period $${T_s}$$ = 1/(3B) sec. Assuming natural sampling and that the pulse amplitude and pulse width are A volts and 1/(30B) sec, respectively, obtain an expression for the frequency spectrum of the sampled signal $${m_s}$$(t)
Questions Asked from Sampling (Marks 5)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE Subjects
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Network Theory
Control Systems
Digital Circuits
General Aptitude
Electronic Devices and VLSI
Analog Circuits
Engineering Mathematics
Microprocessors
Communications
Electromagnetics