A gas has a compressibility factor of 0.5 and a molar volume of $0.4 ~\mathrm{dm}^3 \mathrm{~mol}^{-1}$ at a temperature of $800 \mathrm{~K}$ and pressure $\mathbf{x}$ atm. If it shows ideal gas behaviour at the same temperature and pressure, the molar volume will be $\mathbf{y} ~\mathrm{dm}^3 \mathrm{~mol}^{-1}$. The value of $\mathbf{x} / \mathbf{y}$ is __________.

[Use: Gas constant, $\mathrm{R}=8 \times 10^{-2} \mathrm{~L}$ atm $\mathrm{K}^{-1} \mathrm{~mol}^{-1}$ ]

The plot of $\log k_f$ versus $1 / T$ for a reversible reaction $\mathrm{A}(\mathrm{g}) \rightleftharpoons \mathrm{P}(\mathrm{g})$ is shown.


Pre-exponential factors for the forward and backward reactions are $10^{15} \mathrm{~s}^{-1}$ and $10^{11} \mathrm{~s}^{-1}$, respectively. If the value of $\log K$ for the reaction at $500 \mathrm{~K}$ is 6 , the value of $\left|\log k_b\right|$ at $250 \mathrm{~K}$ is ______.

$$ \begin{aligned} & {[K=\text { equilibrium constant of the reaction }} \\\\ & k_f=\text { rate constant of forward reaction } \\\\ & \left.k_b=\text { rate constant of backward reaction }\right] \end{aligned} $$

One mole of an ideal monoatomic gas undergoes two reversible processes $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ as shown in the given figure:


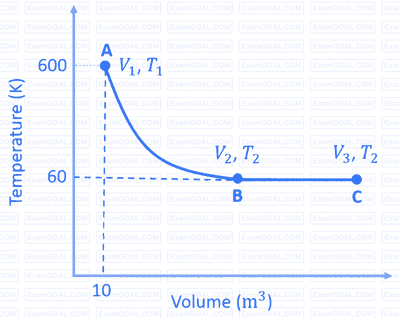
$\mathrm{A} \rightarrow \mathrm{B}$ is an adiabatic process. If the total heat absorbed in the entire process $(\mathrm{A} \rightarrow \mathrm{B}$ and $\mathrm{B} \rightarrow \mathrm{C})$ is $\mathrm{R} T_2 \ln 10$, the value of $2 \log V_3$ is _______.

[Use, molar heat capacity of the gas at constant pressure, $C_{\mathrm{p}, \mathrm{m}}=\frac{5}{2} \mathrm{R}$ ]

In a one-litre flask, 6 moles of $A$ undergoes the reaction $A(\mathrm{~g}) \rightleftharpoons P(\mathrm{~g})$. The progress of product formation at two temperatures (in Kelvin), $\mathrm{T}_1$ and $\mathrm{T}_2$, is shown in the figure:


If $\mathrm{T}_1=2 \mathrm{~T}_2$ and $\left(\Delta \mathrm{G}_2^{\Theta}-\Delta \mathrm{G}_1^{\Theta}\right)=\mathrm{RT}_2 \ln \mathrm{x}$, then the value of $\mathrm{x}$ is _______.

$\left[\Delta \mathrm{G}_1^{\Theta}\right.$ and $\Delta \mathrm{G}_2^{\Theta}$ are standard Gibb's free energy change for the reaction at temperatures $\mathrm{T}_1$ and $\mathrm{T}_2$, respectively.]