Let 𝑥(𝑡) be a periodic function with period 𝑇 = 10. The Fourier series coefficients for this series are denoted by 𝑎_𝑘, that is

$$x\left( t \right) = \sum\limits_{k = - \infty }^\infty {{a_k}} {e^{jk{{2\pi } \over T}t}}$$

The same function 𝑥(𝑡) can also be considered as a periodic function with period T' = 40. Let b_k be the Fourier series coefficients when period is taken as T'. If $$\sum\limits_{k = - \infty }^\infty {\left| {{a_k}} \right|} = 16$$, then $$\sum\limits_{k = - \infty }^\infty {\left| {{b_k}} \right|} = 16$$ is equal to

A periodic signal x(t) has a trigonometric Fourier series expansion $$$x\left(t\right)=a_0\;+\;\sum_{n=1}^\infty\left(a_n\cos\;n\omega_0t\;+\;b_n\sin\;n\omega_0t\right)$$$ If $$x\left(t\right)=-x\left(-t\right)=-x\left(t-\mathrm\pi/{\mathrm\omega}_0\right)$$, we can conclude that

Consider the periodic square wave in the figure shown. 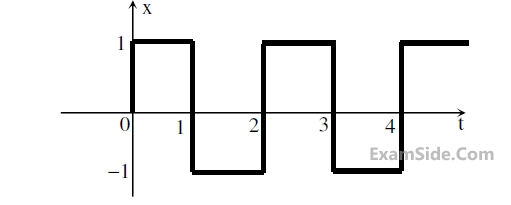The ratio of the power in the 7^th harmonic to the power in the 5^th harmonic for this waveform is closest in value to _______.

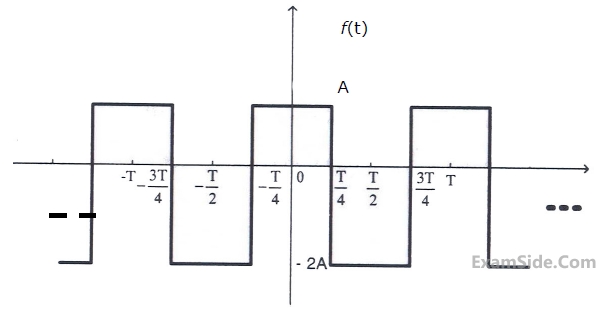
The trigonometric Fourier series for the waveform f(t) shown below contains