In an unbalanced three phase system phase current $${{\rm I}_a} = 1\angle \left( { - {{90}^0}} \right)\,\,pu,\,\,$$ negative sequence current $$\,{{\rm I}_{b2}} = 4\angle \left( { - {{150}^0}} \right)\,\,pu,\,\,$$ zero sequence current $$\,\,{{\rm I}_{c0}} = 3\angle {90^0}\,\,pu.\,\,\,$$ The magnitude of phase current $${{\rm I}_b}$$ in $$pu$ is

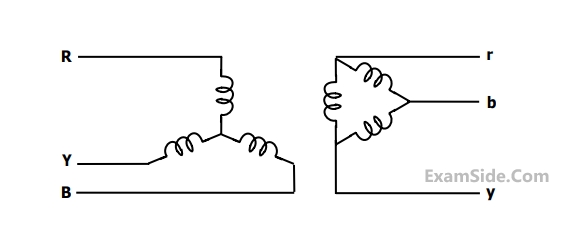
The zero-sequence circuit of the three phase transformer shown in the figure is

Given that: $$\,{V_{s1}} = {V_{s2}} = 1 + j0\,\,p.u,\,\, + ve\,\,$$ sequence impedance are $$\,{Z_{s1}} = {Z_{s2}} = 0.001 + j0.01\,\,p.u\,\,$$ and $${Z_L} = 0.006 + j\,0.06\,\,p.u,\,\,3\phi .\,\,\,$$ Base $$MVA=100,$$ voltage base $$=400$$ $$kV(L-L).$$
Nominal system frequency $$= 50$$ $$Hz.$$ The reference voltage for phase $$'a'$$ is defined as $$\,\,V\left( t \right) = {V_m}\,\cos \left( {\omega t} \right).\,\,\,$$ A symmetrical $$3\phi $$ fault occurs at centre of the line, i.e., at point $$'F'$$ at time 'to' the $$+ve$$ sequence impedance from source $${S_1}$$ to point $$'F'$$ equals $$(0.004 + j \,\,0.04)$$ $$p.u.$$ The wave form corresponding to phase $$'a'$$ fault current from bus $$X$$ reveals that decaying $$d.c.$$ offset current is $$-ve$$ and in magnitude at its maximum initial value. Assume that the negative sequence are equal to $$+ve$$ sequence impedances and the zero sequence $$(Z)$$ are $$3$$ times $$+ve$$ sequence $$(Z).$$

The $$rms$$ value of the ac component of fault current $$\,\left( {{{\rm I}_x}} \right)$$ will be

Given that: $$\,{V_{s1}} = {V_{s2}} = 1 + j0\,\,p.u,\,\, + ve\,\,$$ sequence impedance are $$\,{Z_{s1}} = {Z_{s2}} = 0.001 + j0.01\,\,p.u\,\,$$ and $${Z_L} = 0.006 + j\,0.06\,\,p.u,\,\,3\phi .\,\,\,$$ Base $$MVA=100,$$ voltage base $$=400$$ $$kV(L-L).$$
Nominal system frequency $$= 50$$ $$Hz.$$ The reference voltage for phase $$'a'$$ is defined as $$\,\,V\left( t \right) = {V_m}\,\cos \left( {\omega t} \right).\,\,\,$$ A symmetrical $$3\phi $$ fault occurs at centre of the line, i.e., at point $$'F'$$ at time 'to' the $$+ve$$ sequence impedance from source $${S_1}$$ to point $$'F'$$ equals $$(0.004 + j \,\,0.04)$$ $$p.u.$$ The wave form corresponding to phase $$'a'$$ fault current from bus $$X$$ reveals that decaying $$d.c.$$ offset current is $$-ve$$ and in magnitude at its maximum initial value. Assume that the negative sequence are equal to $$+ve$$ sequence impedances and the zero sequence $$(Z)$$ are $$3$$ times $$+ve$$ sequence $$(Z).$$

Instead of the three phase fault, if a single line to ground fault occurs on phase $$' a '$$ at point $$' F '$$ with zero fault impedance, then the $$rms$$ of the ac component of fault current $$\left( {{{\rm I}_x}} \right)$$ for phase $$'a'$$ will be