Time Response Analysis · Control Systems · GATE EE
Marks 1
Selected data points of the step response of a stable first-order linear time-invariant (LTI) system are given below. The closest value of the time-constant, in sec, of the system is
$$ \begin{array}{|l|c|c|c|c|c|} \hline \text { Time (sec) } & 0.6 & 1.6 & 2.6 & 10 & \infty \\ \hline \text { Output } & 0.78 & 1.65 & 2.18 & 2.98 & 3 \\ \hline \end{array} $$Consider the standard second-order system of the form $\frac{\omega_n^2}{s^2 + 2\zeta\omega_n s + \omega_n^2}$ with the poles $p$ and $p^\ast$ having negative real parts. The pole locations are also shown in the figure. Now consider two such second-order systems as defined below:
System 1: $\omega_n = 3$ rad/sec and $\theta = 60^{\circ}$
System 2: $\omega_n = 1$ rad/sec and $\theta = 70^{\circ}$
Which one of the following statements is correct?

Consider the cascaded system as shown in the figure. Neglecting the faster component of the transient response, which one of the following options is a first-order pole-only approximation such that the steady-state values of the unit step responses of the original and the approximated systems are same?

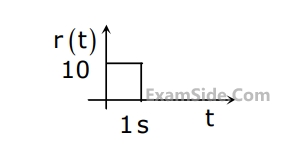
Where $$\delta \left( t \right)$$ is the delta function. Assuming zero initial condition, and denoting the unit step function by $$u(t),y(t)$$ can be of the form
The response of the system as $$\,t \to \infty $$ is

Marks 2
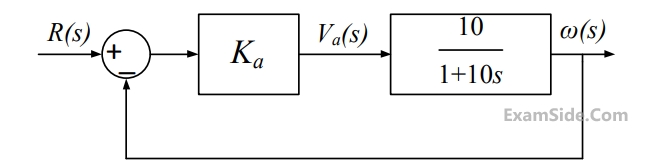
The damping ratio and undamped natural frequency of a closed loop system as shown in the figure, are denoted as $$\xi$$ and $$\omega$$n are

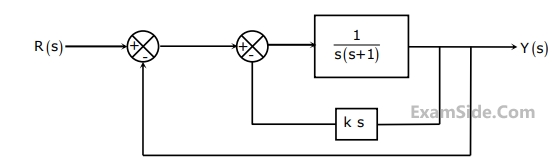
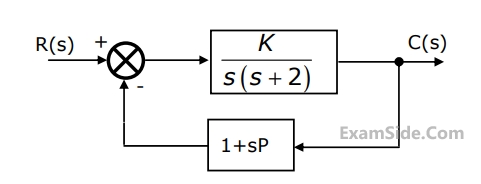
The gain $$k$$ of the Tacho-generator influences mainly the
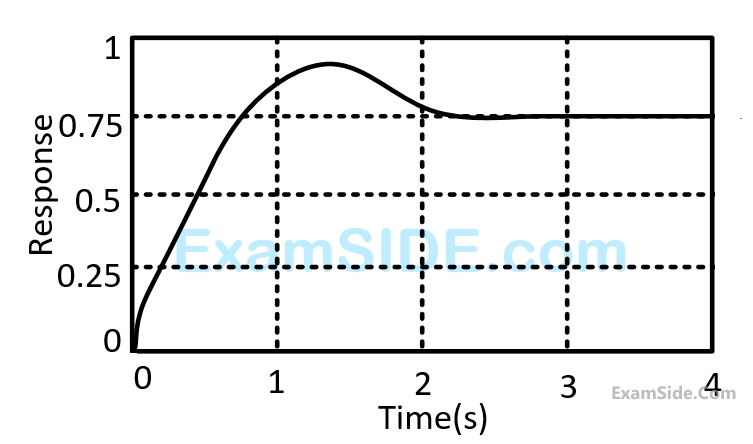
The steady state value of the output of the system for a unit impulse input applied at time instant $$t=1$$ will be

For a step input $${e_{i,}}$$ the overshoot in the output $${e_{0,}}$$ will be

If the above step response is to be observed on a non - storage $$CRO,$$ then it would be best have the $${e_i}$$ as a


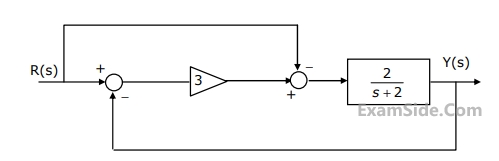
The steady-state value of the unit step response of the system is equal to
The natural time constants of the response of the system are
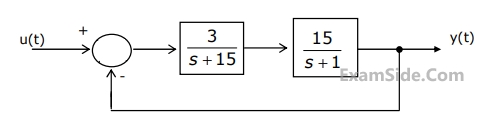
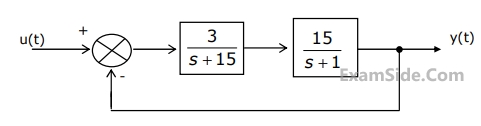

$$a=$$ ____________
$$K=$$ ___________
