Electrostatics · Electromagnetic Fields · GATE EE
Marks 1
Which one of the following figures represents the radial electric field distribution $E_R$ caused by a spherical cloud of electrons with a volume charge density. $\rho=-3 \rho_0$ for $0 \leq R \leq a$ (both $\rho_0, a$ are positive and $R$ is the radial distance) and $\rho=0$ for $R>a$ ?
Take $${\varepsilon _0} = 8.85 \times {10^{ - 12}}$$ F/m.
The Z component of the E field at (0, 0, 0.1) is closest to

 If the potential difference between one of the plates and the nearest surface of dielectric
interface is 2 Volts, then the ratio $$\varepsilon_1\;:\;\varepsilon_2$$ is
If the potential difference between one of the plates and the nearest surface of dielectric
interface is 2 Volts, then the ratio $$\varepsilon_1\;:\;\varepsilon_2$$ is
Marks 2
An air filled cylindrical capacitor (capacitance $C_0$ ) of length $L$, with $a$ and $b$ as its inner and outer radii, respectively, consists of two coaxial conducting surfaces. Its crosssectional view is shown in Figure (i). In order to increase the capacitance, a dielectric material of relative permittivity $\varepsilon_r$ is inserted inside $50 \%$ of the annular region as shown in figure (ii). The value of $\varepsilon_r$ for which the capacitance of the capacitor in figure (ii), becomes $5 C_0$ is

In the $(x, y, z)$ coordinate system, three point-charges $Q$, $Q$, and $\alpha Q$ are located in free space at $(-1, 0, 0)$, $(1, 0, 0)$, and $(0, -1, 0)$, respectively. The value of $\alpha$ for the electric field to be zero at $(0, 0.5, 0)$ is _________________ (rounded off to 1 decimal place).
The closed curve shown in the figure is described by
$$r = 1 + \cos \theta $$, where $$r = \sqrt {{x^2} + {y^2}} ;x = r\cos \theta ,y = r\sin \theta $$The magnitude of the line integral of the vector field $$F = - y\widehat i + x\widehat j$$ around the closed curve is ___________ (Round off to 2 decimal places).

A quadratic function of two variables is given as
$$f({x_1},{x_2}) = x_1^2 + 2x_2^2 + 3{x_1} + 3{x_2} + {x_1}{x_2} + 1$$
The magnitude of the maximum rate of change of the function at the point (1, 1) is ___________ (Round off to the nearest integer).
As shown in the figure below, to concentric conducting spherical shells, centred at r = 0 and having radii r = c and r = d are maintained at potentials such that the potential V(r) at r = c is V1 and V(r) at r = d is V2. Assume that V(r) depends only on r, where r is the radial distance. The expression for V(r) in the region between r = c and r = d is






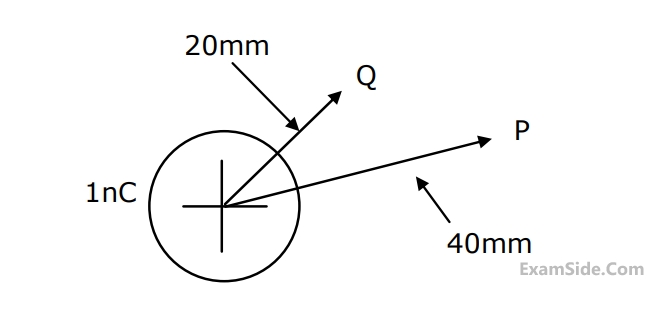

Marks 5
