Linear Time Invariant Systems · Signals and Systems · GATE EE
Marks 1
Consider a discrete-time linear time-invariant (LTI) system, $\boldsymbol{S}$, where
$$ y[n]=S\{x(\mathrm{n})\} $$
$$Let\,\,\,\, S\{\delta[n]\}=\left\{\begin{array}{lc} 1, & n \in\{0,1,2\} \\ 0, & \text { otherwise } \end{array}\right. $$
where $\delta[n]$ is the discrete-time unit impulse function. For an input signal $x[n]$, the output $y[n]$ is
Suppose signal $y(t)$ is obtained by the time-reversal of signal $x(t)$, i.e., $y(t) = x(-t)$, $-\infty < t < \infty$. Which one of the following options is always true for the convolution of $x(t)$ and $y(t)$?
Which of the following statement(s) is/are true?
For the signals $$x(t)$$ and $$y(t)$$ shown in the figure, $$z(t)=x(t)*y(t)$$ is maximum at $$t=T_1$$. Then $$T_1$$ in seconds is __________ (Round off to the nearest integer)


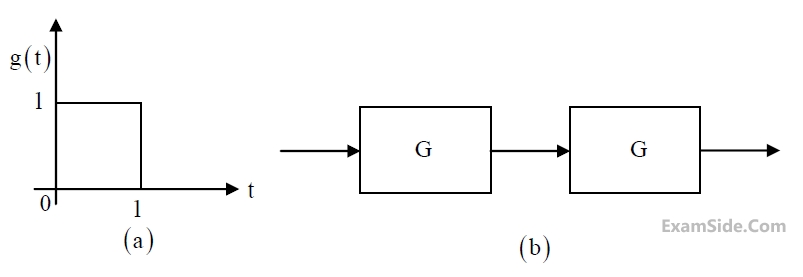
Statement-$$\left( {\rm I} \right)$$: Principle of superposition holds
Statement-$$\left( {\rm II} \right)$$: $$h\left( t \right) = 0$$ for $$t < 0$$
Which one of the following statements is correct?
Marks 2
The input $x(t)$ and the output $y(t)$ of a system are related as
$$ y(t) = e^{-t} \int\limits_{-\infty}^{t} e^{\tau} x(\tau) d\tau, \quad - \infty < t < \infty. $$
The system is
Consider the discrete-time systems $T_1$ and $T_2$ defined as follows:
{ $T_1 x[ n ] = x[ 0 ] + x[ 1 ] + \cdots + x[ n ] $}
{ $T_2 x[ n ] = x[ 0 ] + \frac{1}{2} x[ 1 ] + \cdots + \frac{1}{2^n} x[ n ] $}
Which one of the following statements is true?
Let a causal LTI system be governed by the following differential equation $$y(t) + {1 \over 4}{{dy} \over {dt}} = 2x(t)$$, where x(t) and y(t) are the input and output respectively. Its impulse response is
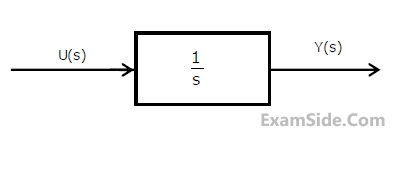
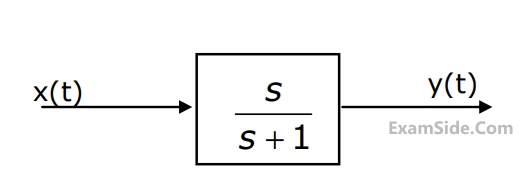
Consider the system as shown below:

where y(t) = x(et). The system is
$$y\left( t \right) = \int\limits_{ - \infty }^{ - 2t} {x\left( \tau \right)} d\tau .$$ The system will be
$$g\left( 0 \right) = 0,\,\,g\left( 1 \right) = g\left( 2 \right) = 1,\,g\left( 3 \right) = g\left( 4 \right) = .... = 0$$
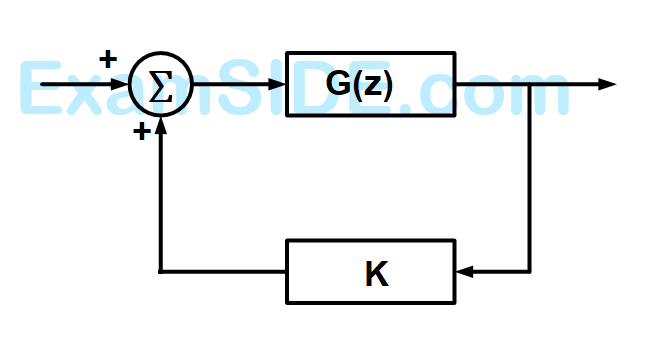
This system is stable for range of values of $$K$$
$$G\left( z \right) = a{z^{ - 1}} + \beta \,\,{z^{ - 3}}$$ is a low-pass digital filter with a phase characteristic same as that of the above question if
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2$$ is the input and
$$y\left[ n \right] = 0;\,n < - 1,\,n > 2,\,y\left[ { - 1} \right] = - 1,\, = y\left[ 1 \right],\,y\left[ 0 \right] = 3,\,y\left[ 2 \right]$$
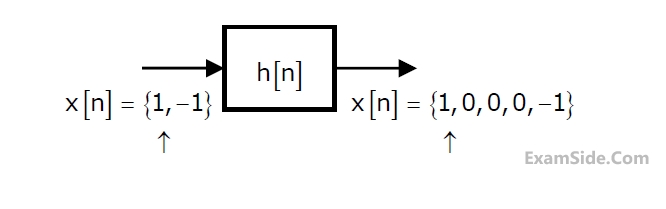
$$\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, =- 2$$ is the output of a discrete-time $$LTI$$ system. The system impulse response $$h\left[ n \right]$$ will be
$$y\left( t \right) = \int\limits_0^t {\left( {2 + t - \tau } \right){e^{ - 3\left( {t - \tau } \right)}}} u\left( \tau \right)d\tau $$
the transfer function $$Y\left( s \right)/U\left( s \right)$$ is
Marks 4
Marks 5
For the above system find an input $$u(t),$$ with zero initial condition, that produces the same output as with no input and with the initial conditions.
$${{d\,y\left( {{0^ - }} \right)} \over {dt}} = - 4,\,\,\,y\left( {{0^ - }} \right) = 1$$



