Power System Stability · Power System Analysis · GATE EE
Marks 1
Marks 2
In the system shown below, the generator was initially supplying power to the grid. A temporary LLLG bolted fault occurs at F very close to circuit breaker-1. The circuit breakers open to isolate the line. The fault self-clears. The circuit breakers reclose and restore the line. Which one of the following diagrams best indicates the rotor accelerating and decelerating areas?

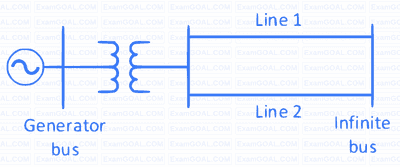
The single line diagram of a lossless system is shown in the figure. The system is operating in steady-state at a stable equilibrium point with the power output of the generator being $P_{max} \sin \delta$, where $\delta$ is the load angle and the mechanical power input is $0.5 P_{max}$. A fault occurs on line 2 such that the power output of the generator is less than $0.5 P_{max}$ during the fault. After the fault is cleared by opening line 2, the power output of the generator is $\left\{\frac{P_{max}}{\sqrt{2}} \right\} \sin \delta$. If the critical fault clearing angle is $\frac{\pi}{2}$ radians, the accelerating area on the power angle curve is ______ times $P_{max}$ (rounded off to 2 decimal places).
Two generating units rated for 250 MW and 400 MW have governor speed regulations of 6% and 6.4%, respectively, from no load to full load. Both the generating units are operating in parallel to share a load of 500 MW. Assuming free governor action, the load shared in MW, by the 250 MW generating unit is ________. (round off to nearest integer).
A 20 MVA, 11.2 kV, 4-pole, 50 Hz alternator has an inertia constant of 15 MJ/MVA. If the input and output powers of the alternator are 15 MW and 10 MW, respectively, the angular acceleration in mechanical degree/s2 is _________. (round off to nearest integer).

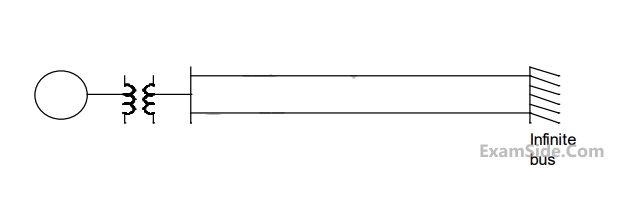
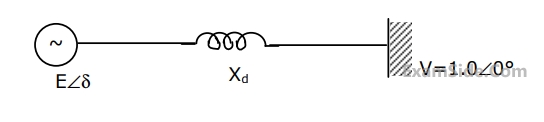
The inertia constant of the synchronous generator $$𝐻 = 5$$ $$MW-s/MVA.$$ Frequency is $$50Hz.$$ Mechanical power is $$1$$ pu. The system is operating at the stable equilibrium point with rotor angle $$\delta $$ equal to $${30^ \circ }$$. A three phase short circuit fault occurs at a certain location on one of the circuits of the double circuit transmission line. During fault, electrical power in pu is $$\,{P_{\max }}\,\,\sin \delta .\,\,\,$$. If the values of $$\delta $$ and $$d$$$$\delta $$$$/dt$$ at the instant of fault clearing are $${45^ \circ }$$ and $$3.762$$ radian/s respectively, then $$\,{P_{\max }}$$ (in pu) is _________.

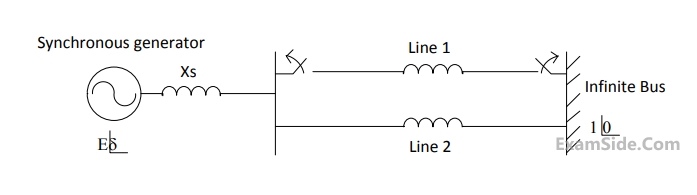
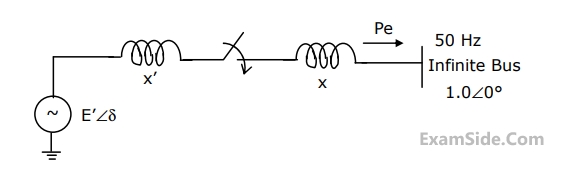
The synchronous generator transfers $$1.0$$ per unit of power to the infinite bus. The critical clearing time of circuit breaker is $$0.28$$ s. If another identical synchronous generator is connected in parallel to the existing generator and each generator is scheduled to supply $$0.5$$ per unit of power, then the critical clearing time of the circuit breaker will

The initial accelerating power (in pu) will be
If the initial accelerating power is $$X$$ pu, the initial acceleration in elect deg/sec2, and the inertia constant in MJ-sec/elect deg respectively will be
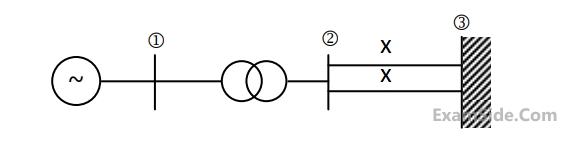
Marks 5
X1 = 0.1 pu, E1 = 1.0 pu, H = 5 MJ/MVA, mechanical power Pm = 0.0 pu, $$\omega $$B = 2 $$\pi \times $$50 rad/sec. All quantities are expressed on a common base.
The generator is initially running on open circuit with the frequency of the open circuit voltage slightly higher than that of the infinite bus. If at the instant of switch closure $$\delta = 0$$ and $$\omega = {{d\delta } \over {dt}} = {\omega _{init}},$$ compute the maximum value of $${\omega _{init}}$$ so that the generator pulls into synchronism.
$$\int {\left( {{{2H} \over {{\omega _B}}}} \right)\omega d\omega + {P_e}d\delta = 0} $$
(i) at the end of an interval
(ii) at the middle of an interval.