Power Generation Cost · Power System Analysis · GATE EE

Marks 1

The incremental cost curves of two generators (Gen A and Gen B) in a plant supplying a common load are shown in the figure. If the incremental cost of supplying the common load is Rs. 7400 per MWh, then the common load in MW is ________ (rounded off to the nearest integer).

GATE EE 2024

If only 5% of the supplied power to a cable reaches the output terminal, the power loss in the cable, in decibels, is ______. (round off to nearest integer).

GATE EE 2022

The figure shows a two-generator system supplying a load of $${P_D} = 40\,MW,$$ connected at bus $$2.$$

The fuel cost of generators $${G_1}$$ and $${G_2}$$ are: $${C_1}\left( {{P_{G1}}} \right) = 10,000\,\,Rs/MWhr$$ and $${C_2}\left( {{P_{G2}}} \right) = 12,500\,\,Rs/MWhr$$ and the loss in the line is $$\,{P_{loss(pu)}} = 0.5\,\,P_{G1\left( {pu} \right),}^2\,\,\,\,$$ where the loss coefficient is specified in pu on a $$100$$ $$MVA$$ base. The most economic power generation schedule in $$MW$$ is

GATE EE 2012

The incremental cost curves in Rs/MWhr for two generators supplying a common load of $$700$$ MW are shown in the figures. The maximum and minimum generation limits are also indicated. The optimum generation schedule is:

GATE EE 2007

In order to have a lower cost of electrical energy generation,

GATE EE 1995

Marks 2

The fuel cost functions in rupees/hour for two 600 MW thermal power plants are given by

Plant 1 : C₁ = 350 + 6P₁ + 0.004P$$_1^2$$

Plant 2 : C₂ = 450 + aP₂ + 0.003P$$_2^2$$

where P₁ and P₂ are power generated by plant 1 and plant 2, respectively, in MW and a is constant. The incremental cost of power ($$\lambda$$) is 8 rupees per MWh. The two thermal power plants together meet a total power demand of 550 MW. The optimal generation of plant 1 and plant 2 in MW, respectively, are

GATE EE 2022

Consider the economic dispatch problem for a power plant having two generating units. The fuel costs in $$Rs/MWh$$ along with the generation limits for the two units are given below:
$$\eqalign{ & {C_1}\left( {{P_1}} \right) = 0.01\,P_1^2 + 30{P_1} + 10; \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,100\,MW \le {P_1} \le 150\,MW \cr} $$
$$\eqalign{ & {C_2}\left( {{P_2}} \right) = 0.05\,P_2^2 + 10{P_2} + 10; \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,100\,MW \le {P_2} \le 180\,MW \cr} $$

The incremental cost (in $$Rs/MWh$$) of the power plant when it supplies $$200$$ $$MW$$ is __________.

GATE EE 2015 Set 1

The incremental costs (in rupees/$$MWh$$) of operating two generating units are functions of their respective powers $${P_1}$$ and $${P_2}$$ in $$MW,$$ and are given by $$${{d{C_1}} \over {d{P_1}}} = 0.2{P_1} + 50$$$ $$${{d{C_2}} \over {d{P_2}}} = 0.24{P_2} + 40$$$
Where, $$$\eqalign{ & 20\,MW \le {P_1} \le 150\,MW \cr & 20\,MW \le {P_2} \le 150MW. \cr} $$$
For a certain load demand, $${P_1}$$ and $${P_2}$$ have been chosen such that $$\,\,d{C_1}/d{P_1} = 76\,Rs/MWh\,\,$$ and $$\,d{C_2}/d{P_2} = 68.8\,Rs/MWh.\,\,$$ If the generations are rescheduled to minimize the total cost, then $${P_2}$$ is ____________.

GATE EE 2015 Set 2

The fuel cost functions of two power plants are
Plant $${P_1}:\,{C_1} = 0.05\,Pg_1^2 + AP{g_1} + B$$
Plant $${P_2}:\,{C_2} = 0.10\,Pg_2^2 + 3AP{g_2} + 2B$$
Where, $$P{g_1}$$ and $$P{g_2}$$ are the generator powers of two plants and $$A$$ and $$B$$ are the constants. If the two plants optimally share $$1000$$ $$MW$$ load at incremental fuel cost of $$100$$ $$Rs/MWh,$$ the ratio of load shared by plants $${P_1}$$ and $${P_2}$$ is

GATE EE 2014 Set 1

A load center of 120 MW derives power from two power stations connected by 220 kV transmission lines of 25 km and 75 km as shown in the figure below. The three generators G1,G2 and G3 are of 100 MW capacity each and have identical fuel cost characteristics. The minimum loss generation schedule for supplying the 120 MW load is

GATE EE 2011

Three generators are feeding a load of $$100$$ $$MW$$. The details of the generators Rating, Efficiency and Regulation are shown below

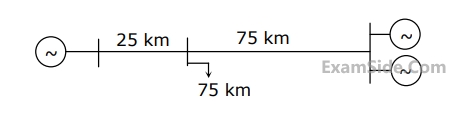
In the event of increased load power demand, which of the following will happen?

GATE EE 2009

A lossless power system has to serve a load of $$250$$ $$MW.$$ There are two generators ($$G1$$ and $$G2$$) in the system with cost curves $${C_1}$$ and $${C_2}$$ respectively defined as follows:
$${C_1}\left( {{P_{G1}}} \right) = {P_{G1}} + 0.055 \times P_{G1}^2$$
$${C_2}\left( {{P_{G2}}} \right) = 3{P_{G2}} + 0.03 \times P_{G2}^2$$
Where $${P_{G1}}$$ and $${P_{G2}}$$ are the MW injections from generator $${G_1}$$ and $${G_2}$$ respectively. Thus, the minimum cost dispatch will be

GATE EE 2008

A load centre is at an equidistant from the two thermal generating stations $${G_1}$$ and $${G_2}$$ as shown in figure. The fuel cost characteristics of the generating stations are given by
$${F_1} = a + b{P_1} + cP_1^2\,Rs/hour$$
$${F_2} = a + b{P_2} + 2cP_2^2\,Rs/hour$$

Where $${P_1}$$ and $${P_2}$$ are the generations in $$MW$$ of $${G_1}$$and $${G_2}$$, respectively. For most economic generation to meet $$300MW$$ of load $${P_1}$$ and $${P_2},$$ respectively, are

GATE EE 2005

Incremental fuel costs (in some appropriate unit) for a power plant consisting of three generating units are
$${\rm I}{C_1} = 20 + 0.3\,\,{P_1},\,{\rm I}{C_2} = 30 + 0.4\,\,{P_2},\,{\rm I}{C_3} = 30$$
Assume that all the three units are operating all the time. Minimum and maximum loads on each unit are $$50$$ $$MW$$ and $$300$$ $$MW$$ respectively. If the plant is operating on economic load dispatch to supply the total power demand of $$700$$ $$MW$$, the power generated by each unit is

GATE EE 2003

The incremental cost characteristic of two generators delivering $$200$$ $$MW$$ are as follows $$\,\,\,{{d{F_1}} \over {d{P_1}}} = 20 + 0.1{P_1},\,\,{{d{F_2}} \over {d{P_2}}} = 16 + 0.2{P_2}$$
For economic operation, the generations $${P_1}$$ and $${P_2}$$ should be

GATE EE 2000

An industrial consumer has a daily load pattern of $$2000$$ $$kW$$, $$0.8$$ lag for $$12$$ Hrs. and $$1000$$ $$kW$$ $$UPF$$ for $$12$$ Hrs. The load factor is

GATE EE 1999

Marks 5

A power system has two generators with the following cost curves
Generator $$1:$$ $${C_1}\left( {{P_{G1}}} \right) = 0.006\,P_{G1}^2 + 8{P_{G1}} + 350$$ (Thousand Rupees/Hour)
Generator $$2:$$ $${C_2}\left( {{P_{G2}}} \right) = 0.006\,P_{G2}^2 + 7{P_{G2}} + 400$$ (Thousand Rupees/Hour)
The generator limits are
$$\eqalign{ & 100\,MW \le {P_{G1}} \le 650\,MW \cr & 50\,MW \le {P_{G2}} \le 500\,MW \cr} $$

A load demand of $$600$$ $$MW$$ is supplied by the generators in an optimal manner. Neglecting losses in the transmission network, determine the optimal generation of each generator.

GATE EE 2001

In a power system, the fuel inputs per hour of plants $$1$$ and $$2$$ are given as
$${F_1} = 0.20\,P_1^2 + 30\,{P_1} + 100\,\,$$ Rs per hour
$${F_2} = 0.25\,P_2^2 + 40\,{P_2} + 150\,\,$$

The limits of generators are $$$\eqalign{ & 20 \le {P_1} \le 80\,MW \cr & 40 \le {P_2} \le 200\,MW \cr} $$$
Find the economic operating schedule of generation, If the load demand is $$130$$ $$MW.$$ neglecting transmission losses.

GATE EE 1998