Polar Nyquist and Bode Plot · Control Systems · GATE EE
Marks 1
The Nyquist plot of a strictly stable $G(s)$ having the numerator polynomial as $(s-3)$ encircles the critical point -1 once in the anti-clockwise direction. Which one of the following statements on the closed-loop system shown in figure, is correct?

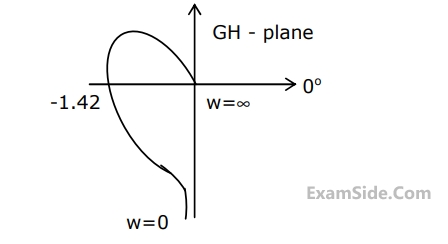
In the Nyquist plot of the open-loop transfer function
$$G(s)H(s) = {{3s + 5} \over {s - 1}}$$
corresponding to the feedback loop shown in the figure, the infinite semi-circular arc of the Nyquist contour in s-plane is mapped into a point at

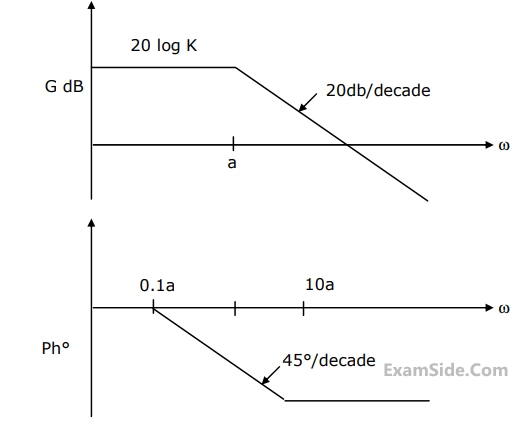
The Bode magnitude plot of a first order stable system is constant with frequency. The asymptotic value of the high frequency phase, for the system, is $$-$$180$$^\circ$$. This system has

Let the output of the system be $${v_0}\left( t \right) = {v_m}\sin \left( {\omega t + \phi } \right)$$ for the input $${v_i}\left( t \right) = {v_m}\sin \left( {\omega t} \right).$$ Then the minimum and maximum values of ϕ (in radians) are respectively

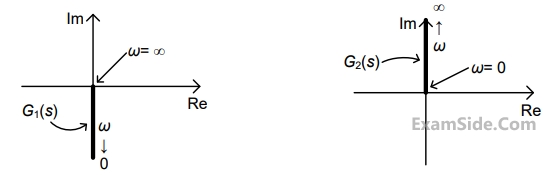
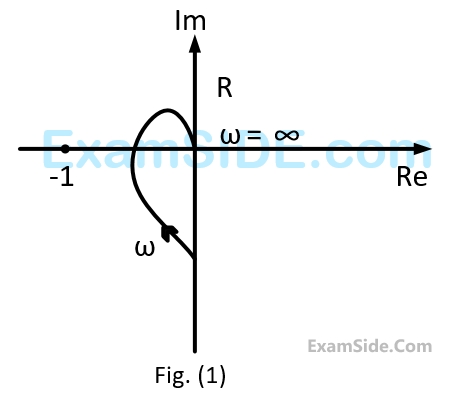
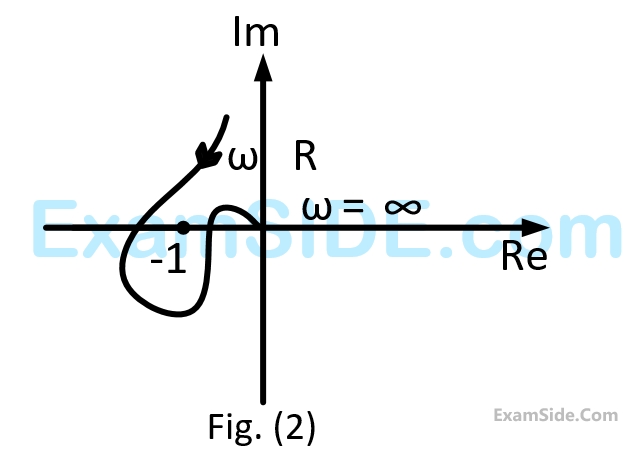
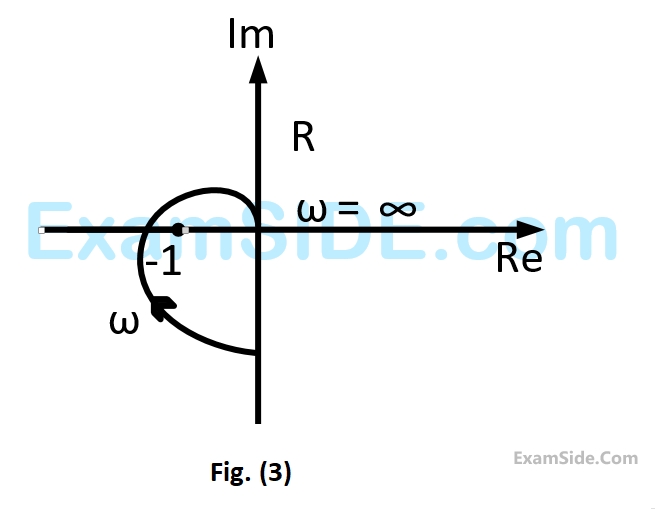
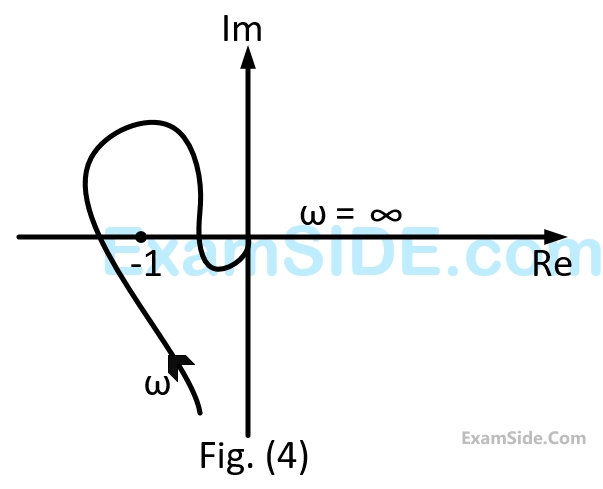
Nyquist plot of the product of $${G_1}\left( s \right)$$ and $${G_2}\left( s \right)$$ is
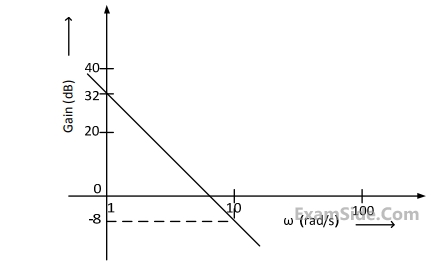
The gain is $$\left( {20\log \left| {G\left( s \right)} \right|} \right)$$ is $$32$$ $$dB$$ and $$–8$$ $$dB$$ at $$1$$ $$rad/s$$ and $$10$$ $$rad/s$$ respectively. The phase is negative for all $$\omega .$$ Then $$G(s)$$ is

The gain margin and phase margin of the system are


For the input $$\,r\left( t \right)\,\, = \,\,\sin \,t,$$ the steady state value of $$c(t)$$ is equal to
The Nyquist plot of $$G$$ encircle the origin


Marks 2
Consider the stable closed-loop system shown in the figure. The asymptotic Bode magnitude plot of $G(s)$ has a constant slope of $-20$ dB/decade at least till $100$ rad/sec with the gain crossover frequency being $10$ rad/sec. The asymptotic Bode phase plot remains constant at $-90^{o}$ at least till $\omega = 10$ rad/sec. The steady-state error of the closed-loop system for a unit ramp input is ________________ (rounded off to 2 decimal places).

Consider the stable closed-loop system shown in the figure. The magnitude and phase values of the frequency response of $G(s)$ are given in the table. The value of the gain $K_I$ ($>0$) for a $50^\circ$ phase margin is _____ (rounded off to 2 decimal places).
| $\omega$ in rad/sec | Magnitude in dB | Phase in degrees |
|---|---|---|
| 0.5 | −7 | −40 |
| 1.0 | −10 | −80 |
| 2.0 | −18 | −130 |
| 10.0 | −40 | −200 |

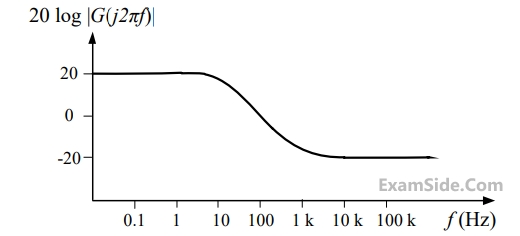
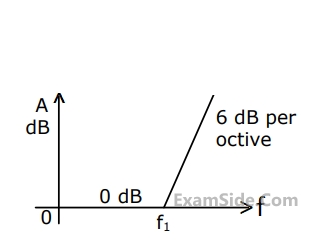
The magnitude and phase plots of an LTI system are shown in the figure. The transfer function of the system is

Consider a lead compensator of the form
$$K(s) = {{1 + {s \over a}} \over {1 + {s \over {\beta a}}}},\beta > 1,a > 0$$
The frequency at which this compensator produces maximum phase lead is 4 rad/s. At this frequency, the gain amplification provided by the controller, assuming asymptotic Bode-magnitude plot of $$K(s)$$, is 6 dB. The values of $$a,\beta$$, respectively, are
An LTI system is shown in the figure where $$G(s) = {{100} \over {{s^2} + 0.1s + 100}}$$. The steady state output of the system, to the input r(t), is given as y(t) = a + b sin(10t + $$\theta$$). The values of a and b will be

The open loop transfer function of a unity gain negative feedback system is given as
$$G(s) = {1 \over {s(s + 1)}}$$
The Nyquist contour in the s-plane encloses the entire right half plane and a small neighbourhood around the origin in the left half plane, as shown in the figure below. The number of encirclements of the point ($$-$$1 + j0) by the Nyquist plot of G(s), corresponding to the Nyquist contour, is denoted as N. Then N equals to

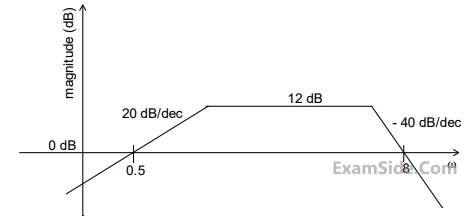
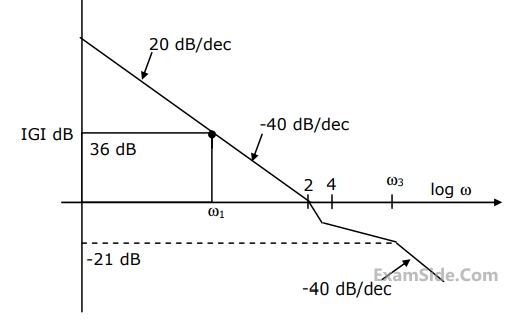
Which one of the following transfer functions is best represented by the above Bode magnitude plot?
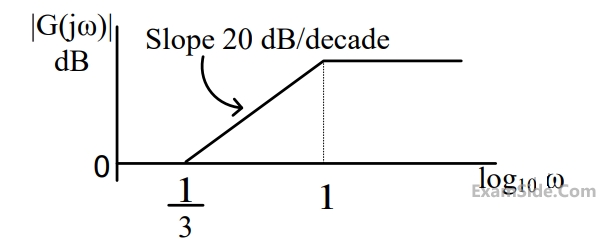
The maximum phase angle $${\phi _m}$$ and the corresponding gain $${G_m}$$ respectively are
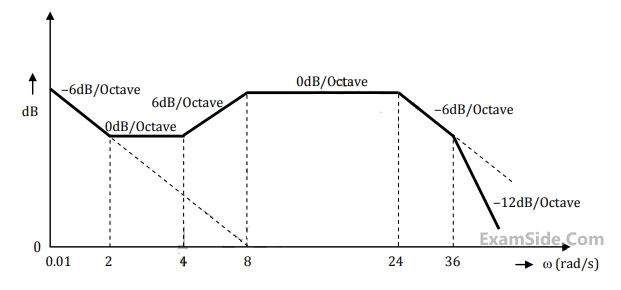

The gain margin of this system is

This transfer function has
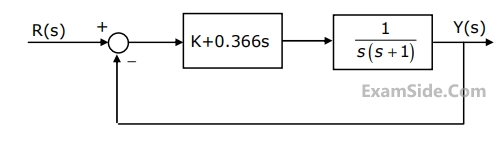

Marks 5
(a) Determine the magnitude of $$G\left( {j\omega } \right)$$ in dB at an angular frequency of $$\omega = 20rad/\sec .$$
(b) Determine the phase margin in degrees.
(c) Determine the gain margin in $$dB.$$
(d) Is the system stable or unstable?
Given : $$\,\left| {{G_1}\left( {j\omega } \right)} \right| \approx 1$$ when $$\omega = 0.446$$
(a) Determine the phase margin when $${\tau _D} = 0$$
(b) Comment in one sentence on the effect of dead time on the stability of the system.
(c) Determine the maximum value of dead time $${\tau _D}$$ for the closed-loop system to be stable.