Continuous Time Signal Fourier Transform · Signals and Systems · GATE EE
Marks 1
1
Let $X(\omega)$ be the Fourier transform of the signal
$x(t) = e^{-t^4} \cos t, \quad -\infty < t < \infty$.
The value of the derivative of $X(\omega)$ at $\, \omega = 0$ is ______ (rounded off to 1 decimal place).
GATE EE 2024
2
A function f(t) is shown in the figure.
The Fourier transform F($$\mathrm\omega$$) of f(t) is
The Fourier transform F($$\mathrm\omega$$) of f(t) is
GATE EE 2014 Set 3
3
A signal is represented by $$$x\left(t\right)=\left\{\begin{array}{l}1\;\;\;\left|t\right|\;<\;1\\0\;\;\;\left|t\right|\;>\;1\end{array}\right.$$$
The Fourier transform of the convolved signal y(t)=x(2t) * x(t/2) is
GATE EE 2014 Set 3
Marks 2
1
An ideal low pass filter has frequency response given by
$$
H(j \omega)= \begin{cases}1, & |\omega| \leq 200 \pi \\ 0, & \text { otherwise }\end{cases}
$$
Let $h(t)$ be its time domain representation. Then $h(0)=$ ____________ (round off to the nearest integer)
GATE EE 2025
2
Let an input x(t) = 2 sin(10$$\pi$$t) + 5 cos(15$$\pi$$t) + 7 sin(42$$\pi$$t) + 4 cos(45$$\pi$$t) is passed through an LTI system having an impulse response,
$$h(t) = 2\left( {{{\sin (10\pi t)} \over {\pi t}}} \right)\cos (40\pi t)$$
The output of the system is
GATE EE 2022
3
Let $f(t)$ be an even function, i.e., $f(-t)=f(t)$ for all $t$. Let the Fourier transform of $f(t)$ be defined as
$F(\omega)=\int_{-\infty}^{\infty} f(t) e^{-j \omega t} d t$. Suppose $\frac{d F(\omega)}{d \omega}=-\omega F(\omega)$ for all $\omega$ and $F(0)=1$. Then
GATE EE 2021
4
Consider a continuous time signal $x(t)$ defined by $x(t)=0$ for $|t|>1$ and $x(t)=1-|t|$ for $|t| \leq 1$
Let the Fourier transform of $x(t)$ be defined as $X(\omega)=\int_{-\infty}^{\infty} x(t) e^{-j \omega t} d t$. The maximum magnitude of $X(\omega)$ is $\_\_\_\_$ .
GATE EE 2021
5
Suppose x1(t) and x2(t) have the Fourier transforms as shown below.
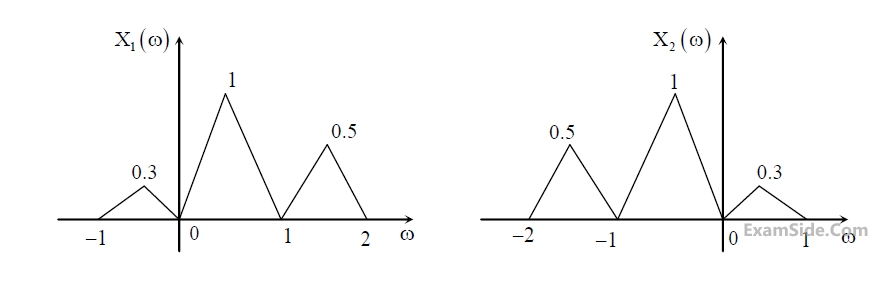Which one of the following statements is TRUE?
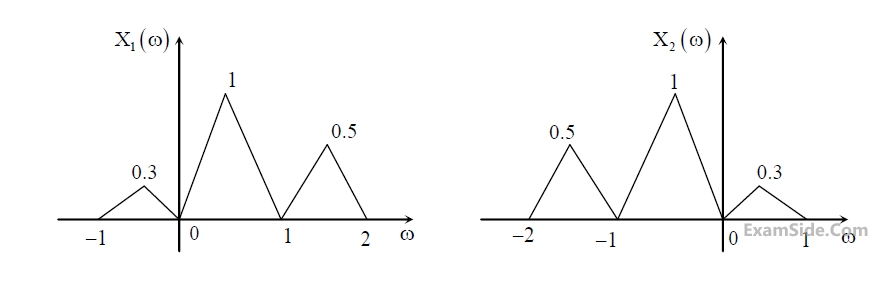Which one of the following statements is TRUE?GATE EE 2016 Set 1
6
Consider a signal defined by $$$x\left(t\right)=\left\{\begin{array}{l}e^{j10t}\;\;\;for\;\left|t\right|\leq1\\0\;\;\;\;\;\;\;for\;\;\left|t\right|>1\end{array}\right.$$$
Its Fourier Transform is
GATE EE 2015 Set 2
7
A differentiable non constant even function x(t) has a derivative y(t), and their respective
Fourier Transforms are X($$\omega$$) and Y($$\omega$$). Which of the following statements is TRUE?
GATE EE 2014 Set 3
8
A 10 kHz even-symmetric square wave is passed through a bandpass filter with centre
frequency at 30 kHz and 3 dB passband of 6 kHz. The filter output is
GATE EE 2014 Set 2
9
Let f(t) be a continuous time signal and let F($$\omega$$) be its Fourier Transform defined by $$F\left(\omega\right)=\int_{-\infty}^\infty f\left(t\right)e^{-j\omega t}dt$$. Define g(t) by $$g\left(t\right)=\int_{-\infty}^\infty F\left(u\right)e^{-jut}du$$. What is the relationship between f(t) and g(t)?
GATE EE 2014 Set 1
10
The Fourier transform of a signal h(t) is $$H\left(j\omega\right)=\left(2\cos\omega\right)\left(\sin2\omega\right)/\omega$$. The value of h(0) is
GATE EE 2012
11
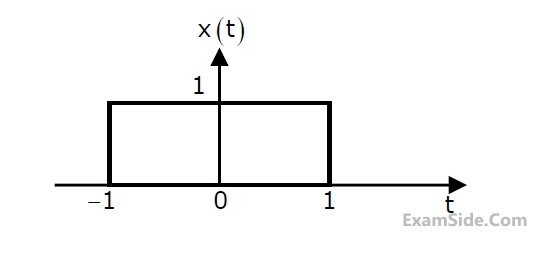
x(t) is a positive rectangular pulse from t = -1 to t = +1 with unit height as shown
in the figure. The value of $$\int_{-\infty}^\infty\left|X\left(\omega\right)\right|^2d\omega$$ {where X($$\mathrm\omega$$) is the Fourier transform of
x(t)} is
GATE EE 2010