Continuous and Discrete Time Signals · Signals and Systems · GATE EE
Marks 1
Consider a continuous-time signal
$$ x(t)=-t^2\{u(t+4)-u(t-4)\} $$
where $u(t)$ is the continuous-time unit step function. Let $\delta(t)$ be the continuous-time unit impulse function. The value of
$$ \int_{-\infty}^{\infty} x(t) \delta(t+3) d t $$
is
A continuous-time system that is initially at rest is described by
$${{dy(t)} \over {dt}} + 3y(t) = 2x(t)$$,
where $$x(t)$$ is the input voltage and $$y(t)$$ is the output voltage. The impulse response of the system is
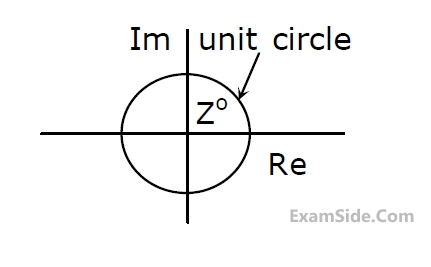The plot of the complex number $$y=\frac1z$$ isMarks 2
Let continuous-time signals $x_1(t)$ and $x_2(t)$ be
$x_1(t)=\left\{\begin{array}{cc}1, & t \in[0,1] \\ 2-t, & t \in[1,2] \\ 0, & \text { otherwise }\end{array}\right.$
and $x_2(t)=\left\{\begin{array}{cc}t, & t \in[0,1] \\ 2-t, & t \in[1,2] \\ 0, & \text { otherwise }\end{array}\right.$.
$y(t)=x_1(t) * x_2(t)$. Then $\int\limits_{-\infty}^{\infty} y(t) d t$ is :
If the energy of a continuous-time signal $x(t)$ is $E$ and the energy of the signal $2x(2t - 1)$ is $cE$, then $c$ is _____ (rounded off to 1 decimal place).
The period of the discrete-time signal $$x[n]$$ described by the equation below is $$N=$$ __________ (Round off to the nearest integer).
$$x[n] = 1 + 3\sin \left( {{{15\pi } \over 8}n + {{3\pi } \over 4}} \right) - 5\sin \left( {{\pi \over 3}n - {\pi \over 4}} \right)$$
