1
GATE ECE 2006
MCQ (Single Correct Answer)
+2
-0.6
A signal m(t) with bandwidth 500 Hz is first multiplied by a signal g(t) where $$g(t)\, = \,\,\sum\limits_{k = - \infty }^\infty {{{( - 10)}^k}\,\delta (t - 0.5x{{10}^{ - 4}}k)} $$
The resulting signal is then passed through an ideal low pass filter with bandwidth 1 kHz. The output of the low pass filter would be
The resulting signal is then passed through an ideal low pass filter with bandwidth 1 kHz. The output of the low pass filter would be
2
GATE ECE 2004
MCQ (Single Correct Answer)
+2
-0.6
A 1 kHz sinusoidal signal is ideally sampled at 1500 samples /sec and the sampled signal is passed through an ideal low-pass filter with cut-off frequency 800 Hz. The output signal has the frequency
3
GATE ECE 2003
MCQ (Single Correct Answer)
+2
-0.6
Let x(t) = $$\,2\cos (800\pi t) + \cos (1400\pi t)$$. x(t) is sampled with the rectangular pulse train shown in figure. The only spectral components (in KHz) present in the sampled signal in the frequency range 2.5 kHz to 3.5 kHz are
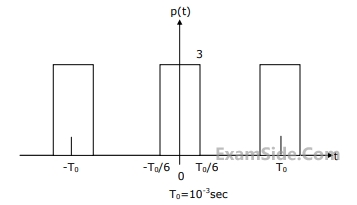

4
GATE ECE 2002
MCQ (Single Correct Answer)
+2
-0.6
A signal x(t) = 100 cos $$(24\pi \times {10^3})$$ t is ideally sampled with a sampling period of 50 $$\mu \sec $$ and then passed through an ideal low pass filter with cutoff frequency of 15 KHz. Which of the following frequencies is/ are present at the filter output?
Questions Asked from Sampling (Marks 2)
Number in Brackets after Paper Indicates No. of Questions
GATE ECE Subjects
Network Theory
Control Systems
Electronic Devices and VLSI
Analog Circuits
Digital Circuits
Microprocessors
Signals and Systems
Representation of Continuous Time Signal Fourier Series Fourier Transform Continuous Time Signal Laplace Transform Discrete Time Signal Fourier Series Fourier Transform Discrete Fourier Transform and Fast Fourier Transform Discrete Time Signal Z Transform Continuous Time Linear Invariant System Discrete Time Linear Time Invariant Systems Transmission of Signal Through Continuous Time LTI Systems Sampling Transmission of Signal Through Discrete Time Lti Systems Miscellaneous
Communications
Electromagnetics
General Aptitude