JEE Advanced 2021 Paper 1 Online
Paper was held on
Sat, Oct 2, 2021 9:00 PM
Chemistry
1
The major product formed in the following reaction of


2
Among the following, the conformation that corresponds to the most stable conformation of meso-butane-2,3-diol is
3
For the given close packed structure of a salt made of cation X and anion Y shown below (ions of only one face are shown for clarity), the packing fraction is approximately (packing fraction = $${{packing\,efficiency} \over {100}}$$)


4
The calculated spin only magnetic moments of [
Cr(NH3)6]3+ and [CuF6]3$$-$$ in BM, respectively, are
(Atomic numbers of Cr and Cu are 24 and 29, respectively)
(Atomic numbers of Cr and Cu are 24 and 29, respectively)
5
For the following reaction scheme, percentage yields are given along the arrow:

x g and y g are mass of R and U, respectively.
(Use : Molar mass (in g mol$$-$$1) of H, C and O as 1, 12 and 16, respectively)
The value of x is ________.

x g and y g are mass of R and U, respectively.
(Use : Molar mass (in g mol$$-$$1) of H, C and O as 1, 12 and 16, respectively)
The value of x is ________.
6
The value of y is ________.
7
The value of standard enthalpy, $$\Delta$$Ho (in kJ mol$$-$$1) for the given reaction is _______.
8
The value of $$\Delta$$S$$\theta$$ (in J K$$-$$1 mol$$-$$1) for the given reaction, at 1000 K is _________.
9
The value of x is ________.
10
The value of | y | is ________.
11
Given :

The compound(s), which on reaction with HNO3 will give the product having degree of rotation, [$$\alpha$$]D = $$-$$52.7$$^\circ$$ is (are)

The compound(s), which on reaction with HNO3 will give the product having degree of rotation, [$$\alpha$$]D = $$-$$52.7$$^\circ$$ is (are)
12
The reaction of Q with PhSNa yields an organic compound (major product) that gives positive Carius test on treatment with Na2O2 followed by addition of BaCl2. The correct option(s) for Q is (are)
13
The correct statement(s) related to colloids is (are)
14
An ideal gas undergoes a reversible isothermal expansion from state I to state II followed by a reversible adiabatic expansion from state II to state III. The correct plot(s) representing the changes from state I to state III is (are)
(p : pressure, V : volume, T : temperature, H : enthalpy, S : entropy)
(p : pressure, V : volume, T : temperature, H : enthalpy, S : entropy)
15
The correct statement(s) related to the metal extraction processes is (are) :
16
A mixture of two salts is used to prepare a solution S, which gives the following results :

The correct option(s) for the salt mixture is (are)

The correct option(s) for the salt mixture is (are)
17
The maximum number of possible isomers (including stereoisomers) which may be formed on mono-bromination of 1-methylcyclohex-1-ene using Br2 and UV light is ___________.
18
In the reaction given below, the total number of atoms having sp2 hybridization in the major product P is _________.


19
The total number of possible isomers for [Pt(NH3)4Cl2]Br2 is ______.
Mathematics
1
Consider a triangle $$\Delta$$ whose two sides lie on the x-axis and the line x + y + 1 = 0. If the orthocenter of $$\Delta$$ is (1, 1), then the equation of the circle passing through the vertices of the triangle $$\Delta$$ is
2
The area of the region
$$\left\{ {\matrix{ {(x,y):0 \le x \le {9 \over 4},} & {0 \le y \le 1,} & {x \ge 3y,} & {x + y \ge 2} \cr } } \right\}$$ is
$$\left\{ {\matrix{ {(x,y):0 \le x \le {9 \over 4},} & {0 \le y \le 1,} & {x \ge 3y,} & {x + y \ge 2} \cr } } \right\}$$ is
3
Consider three sets E1 = {1, 2, 3}, F1 = {1, 3, 4} and G1 = {2, 3, 4, 5}. Two elements are chosen at random, without replacement, from the set E1, and let S1 denote the set of these chosen elements. Let E2 = E1 $$-$$ S1 and F2 = F1 $$\cup$$ S1. Now two elements are chosen at random, without replacement, from the set F2 and let S2 denote the set of these chosen elements.
Let G2 = G1 $$\cup$$ S2. Finally, two elements are chosen at random, without replacement, from the set G2 and let S3 denote the set of these chosen elements.
Let E3 = E2 $$\cup$$ S3. Given that E1 = E3, let p be the conditional probability of the event S1 = {1, 2}. Then the value of p is
Let G2 = G1 $$\cup$$ S2. Finally, two elements are chosen at random, without replacement, from the set G2 and let S3 denote the set of these chosen elements.
Let E3 = E2 $$\cup$$ S3. Given that E1 = E3, let p be the conditional probability of the event S1 = {1, 2}. Then the value of p is
4
Let $\theta_1, \theta_2, \ldots, \theta_{10}$ be positive valued angles (in radian) such that $\theta_1+\theta_2+\cdots+\theta_{10}=2 \pi$. Define the complex numbers $z_1=e^{i \theta_1}, z_k=z_{k-1} e^{i \theta_k}$ for $k=2,3, \ldots, 10$, where $i=\sqrt{-1}$. Consider the statements $P$ and $Q$ given below:
$$P:\left| {{z_2} - {z_1}} \right| + \left| {{z_3} - {z_2}} \right| + ..... + \left| {{z_{10}} - {z_9}} \right| + \left| {{z_1} - {z_{10}}} \right| \le 2\pi $$
$$Q:\left| {z_2^2 - z_1^2} \right| + \left| {z_3^2 - z_2^2} \right| + .... + \left| {z_{10}^2 - z_9^2} \right| + \left| {z_1^2 - z_{10}^2} \right| \le 4\pi $$
Then,
$$P:\left| {{z_2} - {z_1}} \right| + \left| {{z_3} - {z_2}} \right| + ..... + \left| {{z_{10}} - {z_9}} \right| + \left| {{z_1} - {z_{10}}} \right| \le 2\pi $$
$$Q:\left| {z_2^2 - z_1^2} \right| + \left| {z_3^2 - z_2^2} \right| + .... + \left| {z_{10}^2 - z_9^2} \right| + \left| {z_1^2 - z_{10}^2} \right| \le 4\pi $$
Then,
5
Three numbers are chosen at random, one after another with replacement, from the set S = {1, 2, 3, ......, 100}. Let p1 be the probability that the maximum of chosen numbers is at least 81 and p2 be the probability that the minimum of chosen numbers is at most 40.
The value of $${{625} \over 4}{p_1}$$ is ___________.
The value of $${{625} \over 4}{p_1}$$ is ___________.
6
Three numbers are chosen at random, one after another with replacement, from the set S = {1, 2, 3, ......, 100}. Let p1 be the probability that the maximum of chosen numbers is at least 81 and p2 be the probability that the minimum of chosen numbers is at most 40.
The value of $${{125} \over 4}{p_2}$$ is ___________.
The value of $${{125} \over 4}{p_2}$$ is ___________.
7
Let $$\alpha$$, $$\beta$$ and $$\gamma$$ be real numbers such that the system of linear equations
x + 2y + 3z = $$\alpha$$
4x + 5y + 6z = $$\beta$$
7x + 8y + 9z = $$\gamma $$ $$-$$ 1
is consistent. Let | M | represent the determinant of the matrix
$$M = \left[ {\matrix{ \alpha & 2 & \gamma \cr \beta & 1 & 0 \cr { - 1} & 0 & 1 \cr } } \right]$$
Let P be the plane containing all those ($$\alpha$$, $$\beta$$, $$\gamma$$) for which the above system of linear equations is consistent, and D be the square of the distance of the point (0, 1, 0) from the plane P.
The value of | M | is _________.
x + 2y + 3z = $$\alpha$$
4x + 5y + 6z = $$\beta$$
7x + 8y + 9z = $$\gamma $$ $$-$$ 1
is consistent. Let | M | represent the determinant of the matrix
$$M = \left[ {\matrix{ \alpha & 2 & \gamma \cr \beta & 1 & 0 \cr { - 1} & 0 & 1 \cr } } \right]$$
Let P be the plane containing all those ($$\alpha$$, $$\beta$$, $$\gamma$$) for which the above system of linear equations is consistent, and D be the square of the distance of the point (0, 1, 0) from the plane P.
The value of | M | is _________.
8
Let $$\alpha$$, $$\beta$$ and $$\gamma$$ be real numbers such that the system of linear equations
x + 2y + 3z = $$\alpha$$
4x + 5y + 6z = $$\beta$$
7x + 8y + 9z = $$\gamma $$ $$-$$ 1
is consistent. Let | M | represent the determinant of the matrix
$$M = \left[ {\matrix{ \alpha & 2 & \gamma \cr \beta & 1 & 0 \cr { - 1} & 0 & 1 \cr } } \right]$$
Let P be the plane containing all those ($$\alpha$$, $$\beta$$, $$\gamma$$) for which the above system of linear equations is consistent, and D be the square of the distance of the point (0, 1, 0) from the plane P.
The value of D is _________.
x + 2y + 3z = $$\alpha$$
4x + 5y + 6z = $$\beta$$
7x + 8y + 9z = $$\gamma $$ $$-$$ 1
is consistent. Let | M | represent the determinant of the matrix
$$M = \left[ {\matrix{ \alpha & 2 & \gamma \cr \beta & 1 & 0 \cr { - 1} & 0 & 1 \cr } } \right]$$
Let P be the plane containing all those ($$\alpha$$, $$\beta$$, $$\gamma$$) for which the above system of linear equations is consistent, and D be the square of the distance of the point (0, 1, 0) from the plane P.
The value of D is _________.
9
Consider the lines L1 and L2 defined by
$${L_1}:x\sqrt 2 + y - 1 = 0$$ and $${L_2}:x\sqrt 2 - y + 1 = 0$$
For a fixed constant $$\lambda$$, let C be the locus of a point P such that the product of the distance of P from L1 and the distance of P from L2 is $$\lambda$$2. The line y = 2x + 1 meets C at two points R and S, where the distance between R and S is $$\sqrt {270} $$. Let the perpendicular bisector of RS meet C at two distinct points R' and S'. Let D be the square of the distance between R' and S'.
The value of $$\lambda$$2 is __________.
$${L_1}:x\sqrt 2 + y - 1 = 0$$ and $${L_2}:x\sqrt 2 - y + 1 = 0$$
For a fixed constant $$\lambda$$, let C be the locus of a point P such that the product of the distance of P from L1 and the distance of P from L2 is $$\lambda$$2. The line y = 2x + 1 meets C at two points R and S, where the distance between R and S is $$\sqrt {270} $$. Let the perpendicular bisector of RS meet C at two distinct points R' and S'. Let D be the square of the distance between R' and S'.
The value of $$\lambda$$2 is __________.
10
Consider the lines L1 and L2 defined by
$${L_1}:x\sqrt 2 + y - 1 = 0$$ and $${L_2}:x\sqrt 2 - y + 1 = 0$$
For a fixed constant $$\lambda$$, let C be the locus of a point P such that the product of the distance of P from L1 and the distance of P from L2 is $$\lambda$$2. The line y = 2x + 1 meets C at two points R and S, where the distance between R and S is $$\sqrt {270} $$. Let the perpendicular bisector of RS meet C at two distinct points R' and S'. Let D be the square of the distance between R' and S'.
The value of D is __________.
$${L_1}:x\sqrt 2 + y - 1 = 0$$ and $${L_2}:x\sqrt 2 - y + 1 = 0$$
For a fixed constant $$\lambda$$, let C be the locus of a point P such that the product of the distance of P from L1 and the distance of P from L2 is $$\lambda$$2. The line y = 2x + 1 meets C at two points R and S, where the distance between R and S is $$\sqrt {270} $$. Let the perpendicular bisector of RS meet C at two distinct points R' and S'. Let D be the square of the distance between R' and S'.
The value of D is __________.
11
For any 3 $$\times$$ 3 matrix M, let | M | denote the determinant of M. Let
$$E = \left[ {\matrix{ 1 & 2 & 3 \cr 2 & 3 & 4 \cr 8 & {13} & {18} \cr } } \right]$$, $$P = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 0 & 1 \cr 0 & 1 & 0 \cr } } \right]$$ and $$F = \left[ {\matrix{ 1 & 3 & 2 \cr 8 & {18} & {13} \cr 2 & 4 & 3 \cr } } \right]$$
If Q is a nonsingular matrix of order 3 $$\times$$ 3, then which of the following statements is(are) TRUE?
$$E = \left[ {\matrix{ 1 & 2 & 3 \cr 2 & 3 & 4 \cr 8 & {13} & {18} \cr } } \right]$$, $$P = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 0 & 1 \cr 0 & 1 & 0 \cr } } \right]$$ and $$F = \left[ {\matrix{ 1 & 3 & 2 \cr 8 & {18} & {13} \cr 2 & 4 & 3 \cr } } \right]$$
If Q is a nonsingular matrix of order 3 $$\times$$ 3, then which of the following statements is(are) TRUE?
12
Let f : R $$\to$$ R be defined by $$f(x) = {{{x^2} - 3x - 6} \over {{x^2} + 2x + 4}}$$
Then which of the following statements is (are) TRUE?
Then which of the following statements is (are) TRUE?
13
Let E, F and G be three events having probabilities $$P(E) = {1 \over 8}$$, $$P(F) = {1 \over 6}$$ and $$P(G) = {1 \over 4}$$, and let P (E $$\cap$$ F $$\cap$$ G) = $${1 \over {10}}$$. For any event H, if Hc denotes the complement, then which of the following statements is (are) TRUE?
14
For any 3 $$\times$$ 3 matrix M, let |M| denote the determinant of M. Let I be the 3 $$\times$$ 3 identity matrix. Let E and F be two 3 $$\times$$ 3 matrices such that (I $$-$$ EF) is invertible. If G = (I $$-$$ EF)$$-$$1, then which of the following statements is (are) TRUE?
15
For any positive integer n, let Sn : (0, $$\infty$$) $$\to$$ R be defined by $${S_n}(x) = \sum\nolimits_{k = 1}^n {{{\cot }^{ - 1}}\left( {{{1 + k(k + 1){x^2}} \over x}} \right)} $$, where for any x $$\in$$ R, $${\cot ^{ - 1}}(x) \in (0,\pi )$$ and $${\tan ^{ - 1}}(x) \in \left( { - {\pi \over 2},{\pi \over 2}} \right)$$. Then which of the following statements is (are) TRUE?
16
For any complex number w = c + id, let $$\arg (w) \in ( - \pi ,\pi ]$$, where $$i = \sqrt { - 1} $$. Let $$\alpha$$ and $$\beta$$ be real numbers such that for all complex numbers z = x + iy satisfying $$\arg \left( {{{z + \alpha } \over {z + \beta }}} \right) = {\pi \over 4}$$, the ordered pair (x, y) lies on the circle $${x^2} + {y^2} + 5x - 3y + 4 = 0$$, Then which of the following statements is (are) TRUE?
17
For x $$\in$$ R, the number of real roots of the equation $$3{x^2} - 4\left| {{x^2} - 1} \right| + x - 1 = 0$$ is ________.
18
In a triangle ABC, let AB = $$\sqrt {23} $$, BC = 3 and CA = 4. Then the value of $${{\cot A + \cot C} \over {\cot B}}$$ is _________.
19
Let $$\overrightarrow u $$, $$\overrightarrow v $$ and $$\overrightarrow w $$ be vectors in three-dimensional space, where $$\overrightarrow u $$ and $$\overrightarrow v $$ are unit vectors which are not perpendicular to each other and $$\overrightarrow u $$ . $$\overrightarrow w $$ = 1, $$\overrightarrow v $$ . $$\overrightarrow w $$ = 1, $$\overrightarrow w $$ . $$\overrightarrow w $$ = 4
If the volume of the paralleopiped, whose adjacent sides are represented by the vectors, $$\overrightarrow u $$, $$\overrightarrow v $$ and $$\overrightarrow w $$, is $$\sqrt 2 $$, then the value of $$\left| {3\overrightarrow u + 5\overrightarrow v } \right|$$ is ___________.
If the volume of the paralleopiped, whose adjacent sides are represented by the vectors, $$\overrightarrow u $$, $$\overrightarrow v $$ and $$\overrightarrow w $$, is $$\sqrt 2 $$, then the value of $$\left| {3\overrightarrow u + 5\overrightarrow v } \right|$$ is ___________.
Physics
1
The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is
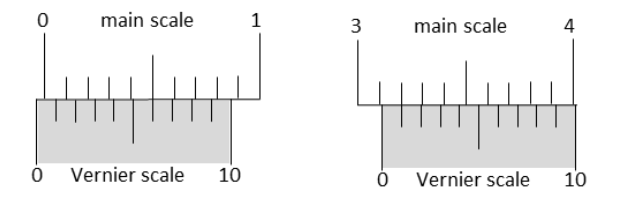

2
An ideal gas undergoes a four step cycle as shown in the P-V diagram below. During this cycle, heat is absorbed by the gas in


3
An extended object is placed at point O, 10 cm in front of a convex lens L1 and a concave lens L2 is placed 10 cm behind it, as shown in the figure. The radii of curvature of all the curved surfaces in both the lenses ae 20 cm. The refractive index of both the lenses is 1.5. The total magnification of this lens system is
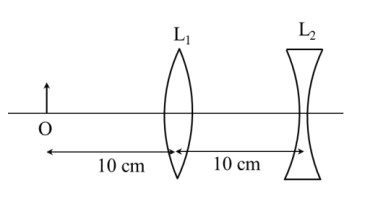

4
A heavy nucleus Q of half-life 20 minutes undergoes alpha-decay with probability of 60% and beta-decay with probability of 40%. Initially, the number of Q nuclei is 1000. The number of alpha-decays of Q in the first one hour is
5
A projectile is thrown from a point O on the ground at an angle 45$$^\circ$$ from the vertical and with a speed 5$$\sqrt 2 $$ m/s. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, 0.5 s after the splitting. The other part, t seconds after splitting, falls to the ground at a distance x meters from the point O. The acceleration due to gravity g = 10 m/s2.
The value of t is _____________.
The value of t is _____________.
6
A projectile is thrown from a point O on the ground at an angle 45$$^\circ$$ from the vertical and with a speed 5$$\sqrt 2 $$ m/s. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, 0.5 s after the splitting. The other part, t seconds after splitting, falls to the ground at a distance x meters from the point O. The acceleration due to gravity g = 10 m/s2.
The value of x is _______________.
The value of x is _______________.
7
In the circuit shown below, the switch S is connected to position P for a long time so that the charge on the capacitor becomes q1 $$\mu$$C. Then S is switched to position Q. After a long time, the charge on the capacitor is q2 $$\mu$$C.

The magnitude of q1 is ________________.

The magnitude of q1 is ________________.
8
In the circuit shown below, the switch S is connected to position P for a long time so that the charge on the capacitor becomes q1 $$\mu$$C. Then S is switched to position Q. After a long time, the charge on the capacitor is q2 $$\mu$$C.

The magnitude of q2 is ________________.

The magnitude of q2 is ________________.
9
Two point charges $$-$$Q and +Q/$$\sqrt 3 $$ are placed in the xy-plane at the origin (0, 0) and a point (2, 0), respectively, as shown in the figure. This results in an equipotential circle of radius R and potential V = 0 in the xy-plane with its center at (b, 0). All lengths are measured in meters.

The value of R is __________ meter.

The value of R is __________ meter.
10
Two point charges $$-$$Q and +Q/$$\sqrt 3 $$ are placed in the xy-plane at the origin (0, 0) and a point (2, 0), respectively, as shown in the figure. This results in an equipotential circle of radius R and potential V = 0 in the xy-plane with its center at (b, 0). All lengths are measured in meters.

The value of b is __________ meter.

The value of b is __________ meter.
11
A horizontal force F is applied at the center of mass of a cylindrical object of mass m and radius R, perpendicular to its axis as shown in the figure. The coefficient of friction between the object and the ground is $$\mu$$. The center of mass of the object has an acceleration a. The acceleration due to gravity is g. Given that the object rolls without slipping, which of the following statement(s) is(are) correct?


12
A wide slab consisting of two media of refractive indices n1 and n2 is placed in air as shown in the figure. A ray of light is incident from medium n1 to n2 at an angle $$\theta$$, where sin$$\theta$$ is slightly larger than 1/n1. Take refractive index of air as 1. Which of the following statement(s) is(are) correct?


13
A particle of mass M = 0.2 kg is initially at rest in the xy-plane at a point (x = $$-$$l, y = $$-$$h), where l = 10 m and h = 1 m. The particle is accelerated at time t = 0 with a constant acceleration a = 10 m/s2 along the positive x-direction. Its angular momentum and torque with respect to the origin, in SI units, are represented by $$\overrightarrow L $$ and $$\overrightarrow \tau $$ respectively. $$\widehat i$$, $$\widehat j$$ and $$\widehat k$$ are unit vectors along the positive x, y and z-directions, respectively. If $$\widehat k$$ = $$\widehat i$$ $$\times$$ $$\widehat j$$ then which of the following statement(s) is(are) correct?
14
Which of the following statement(s) is(are) correct about the spectrum of the hydrogen atom?
15
A long straight wire carries a current, I = 2 ampere. A semi-circular conducting rod is placed beside it on two conducting parallel rails of negligible resistance. Both the rails are parallel to the wire. The wire, the rod and the rails lie in the same horizontal plane, as shown in the figure. Two ends of the semi-circular rod are at the distances 1 cm and 4 cm from the wire. At time t = 0, the rod starts moving on the rails with a speed v = 3.0 m/s (see the figure).
A resistor R = 1.4 $$\Omega$$ and a capacitor C0 = 5.0$$\mu$$F are connected in series between the rails. At time t = 0, C0 is uncharged. Which of the following statement(s) is(are) correct? [$$\mu$$0 = 4$$\pi$$ $$\times$$ 10$$-$$7 SI units. Take ln 2 = 0.7]

A resistor R = 1.4 $$\Omega$$ and a capacitor C0 = 5.0$$\mu$$F are connected in series between the rails. At time t = 0, C0 is uncharged. Which of the following statement(s) is(are) correct? [$$\mu$$0 = 4$$\pi$$ $$\times$$ 10$$-$$7 SI units. Take ln 2 = 0.7]

16
A cylindrical tube, with its base as shown in the figure, is filled with water. It is moving down with a constant acceleration a along a fixed inclined plane with angle $$\theta$$ = 45$$^\circ$$. P1 and P2 are pressures at points 1 and 2, respectively, located at the base of the tube. Let $$\beta$$ = (P1 $$-$$ P2)/($$\rho$$gd), where $$\rho$$ is density of water, d is the inner diameter of the tube and g is the acceleration due to gravity. Which of the following statement(s) is(are) correct?


17
An $$\alpha$$-particle (mass 4 amu) and a singly charged sulphur ion (mass 32 amu) are initially at rest. They are accelerated through a potential V and then allowed to pass into a region of uniform magnetic field which is normal to the velocities of the particles. Within this region, the $$\alpha$$-particle and the sulfur ion move in circular orbits of radii r$$\alpha$$ and rs, respectively. The ratio (rs/r$$\alpha$$) is __________.
18
A thin rod of mass M and length a is free to rotate in horizontal plane about a fixed vertical axis passing through point O. A thin circular disc of mass M and of radius a/4 is pivoted on this rod with its center at a distance a/4 from the free end so that it can rotate freely about its vertical axis, as shown in the figure. Assume that both the rod and the disc have uniform density and they remain horizontal during the motion. An outside stationary observer finds the rod rotating with an angular velocity $$\Omega$$ and the disc rotating about its vertical axis with angular velocity 4$$\Omega$$. The total angular momentum of the system about the point O is $$\left( {{{M{a^2}\Omega } \over {48}}} \right)n$$. The value of n is ___________.


19
A small object is placed at the center of a large evacuated hollow spherical container. Assume that the container is maintained at 0 K. At time t = 0, the temperature of the object is 200 K. The temperature of the object becomes 100 K at t = t1 and 50 K at t = t2. Assume the object and the container to be ideal black bodies. The heat capacity of the object does not depend on temperature. The ratio (t2/t1) is ____________.