IIT-JEE 2011 Paper 2 Offline | JEE Advanced Year Wise Previous Years Questions

IIT-JEE 2011 Paper 2 Offline

Numerical

-1

Let M be a 3 $$\times$$ 3 matrix satisfying $$M\left[ {\matrix{ 0 \cr 1 \cr 0 \cr } } \right] = \left[ {\matrix{ { - 1} \cr 2 \cr 3 \cr } } \right]$$, $$M\left[ {\matrix{ 1 \cr { - 1} \cr 0 \cr } } \right] = \left[ {\matrix{ 1 \cr 1 \cr { - 1} \cr } } \right]$$ and $$M\left[ {\matrix{ 1 \cr 1 \cr 1 \cr } } \right] = \left[ {\matrix{ 0 \cr 0 \cr {12} \cr } } \right]$$. Then the sum of the diagonal entries of M is ___________.

Your input ____

IIT-JEE 2011 Paper 2 Offline

MCQ (Single Correct Answer)

-1

Match the statements given in Column I with the intervals/union of intervals given in Column II :

IIT-JEE 2011 Paper 2 Offline Mathematics - Functions Question 13 English

(A) $$\to$$ (S), (B) $$\to$$ (T), (C) $$\to$$ (P), (D) $$\to$$ (Q)

(A) $$\to$$ (S), (B) $$\to$$ (T), (C) $$\to$$ (R), (D) $$\to$$ (P)

(A) $$\to$$ (S), (B) $$\to$$ (T), (C) $$\to$$ (R), (D) $$\to$$ (R)

(A) $$\to$$ (P), (B) $$\to$$ (Q), (C) $$\to$$ (R), (D) $$\to$$ (R)

IIT-JEE 2011 Paper 2 Offline

MCQ (More than One Correct Answer)

-1

Which of the following statement(s) is/are correct?

If the electric field due to a point charge varies as $${r^{ - 2.5}}$$ instead of $${r^{ - 2}},$$ then the Gauss law will still be valid.

The Gauss law can be used to calculate the field distribution around an electric dipole.

If the electric field between two point charges is zero somewhere, then the sign of the two charges is the same.

The work done by the external force in moving a unit positive charge from point $$A$$ at potential $${V_A}$$ to point $$B$$ at potential $${V_B}$$ is $$\left( {{V_B} - {V_A}} \right).$$

IIT-JEE 2011 Paper 2 Offline

MCQ (Single Correct Answer)

-0.5

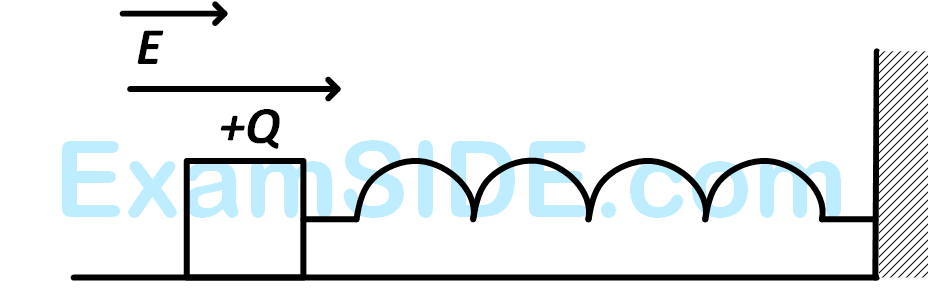
A wooden block performs $$SHM$$ on a frictionless surface with frequency, $${v_0}.$$ The block carries a charge $$+Q$$ on its surface . If now a uniform electric field $$\overrightarrow E $$ is switched- on as shown, then the $$SHM$$ of the block will be
IIT-JEE 2011 Paper 2 Offline Physics - Simple Harmonic Motion Question 23 English

IIT-JEE 2011 Paper 2 Offline Physics - Simple Harmonic Motion Question 23 English

of the same frequency and with shifted mean position.

of the same frequency and with the same mean position

of changed frequency and with shifted mean position.

of changed frequency and with the same mean position.

PREVIOUS NEXT

JEE Advanced Papers

All year-wise previous year question papers

2026