Column I shows four situations of standard Young's double slit arrangement with the screen placed far away from the slits S$$_1$$ and S$$_2$$. In each of these cases, S$$_1$$P$$_0$$ = S$$_2$$P$$_0$$, S$$_1$$P$$_1$$ $$-$$ S$$_2$$P$$_1$$ = $$\lambda/4$$ and S$$_1$$P$$_2$$ $$-$$ S$$_2$$P$$_2$$ = $$\lambda/3$$, where $$\lambda$$ is the wavelength of the light used. In the cases B, C and D, a transparent sheet of refractive index $$\mu$$ and thickness t is pasted on slit S$$_2$$. The thickness of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by $$\delta$$(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation:

	Column I		Column II
(A)		(P)	$$\delta ({P_0}) = 0$$
(B)	$$(\mu-1)t=\lambda/4$$	(Q)	$$\delta ({P_1}) = 0$$
(C)	$$(\mu-1)t=\lambda/2$$	(R)	$$I({P_1}) = 0$$
(D)	$$(\mu-1)t=3\lambda/4$$	(S)	$$I({P_0}) > I({P_1})$$
		(T)	$$I({P_2}) > I({P_1})$$

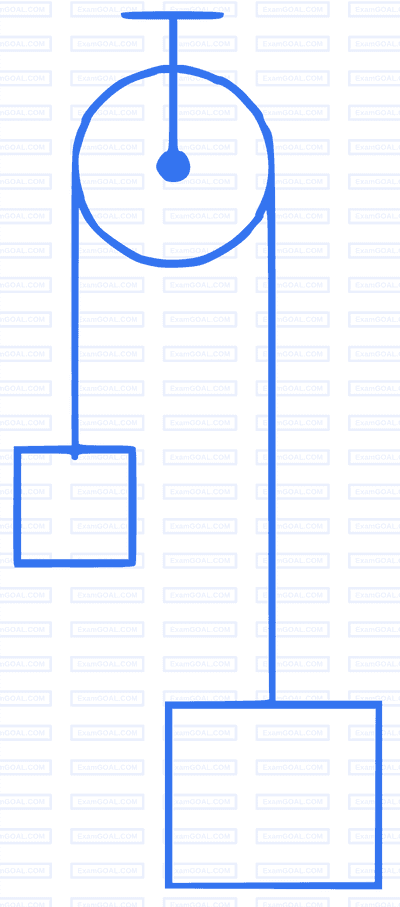
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s², find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.

Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8 N/m$$^2$$. The radii of bubbles A and B are 2 cm and 4 cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. Find the ratio $$n_B/n_A$$, where $$n_A$$ and $$n_B$$ are the number of moles of air in bubbles A and B, respectively. (Neglect the effect of gravity.)

A steady current I goes through a wire loop PQR having shape of a right angle triangle wit6h PQ = 3, PR = 4x and QR = 5x. If the magnitude of the magnetic field at P due to this loop is $$k\left( {{{{\mu _0}I} \over {48\pi x}}} \right)$$, find the value of $$k$$.