Column II gives certain systems undergoing a process. Column I suggests changes in some of the parameters related to the system. Match the statements in Column I to the appropriate process(es) from Column II:
| Column I | Column II | ||
|---|---|---|---|
| (A) | The energy of the system is increased. | (P) | System : A capacitor, initially uncharged. Process : It is connected to a battery. |
| (B) | Mechanical energy is provided to the system, which is converted into energy of random motion of its parts. | (Q) | System : A gas in an adiabatic container filled with an adiabatic piston. Process : The gas is compressed by pushing the piston. |
| (C) | Internal energy of the system is converted into its mechanical energy. | (R) | System : A gas in a rigid container. Process : The gas gets cooled due to colder atmosphere surrounding it. |
| (D) | Mass of the system is decreased. | (S) | System : A heavy nucleus, initially at rest. Process : The nucleus fissions into two fragments of nearly equal masses and some neutrons are emitted. |
| (T) | System : A resistive wire loop. Process : The loop is placed in a time varying magnetic field perpendicular to its plane. |
Column I shows four situations of standard Young's double slit arrangement with the screen placed far away from the slits S$$_1$$ and S$$_2$$. In each of these cases, S$$_1$$P$$_0$$ = S$$_2$$P$$_0$$, S$$_1$$P$$_1$$ $$-$$ S$$_2$$P$$_1$$ = $$\lambda/4$$ and S$$_1$$P$$_2$$ $$-$$ S$$_2$$P$$_2$$ = $$\lambda/3$$, where $$\lambda$$ is the wavelength of the light used. In the cases B, C and D, a transparent sheet of refractive index $$\mu$$ and thickness t is pasted on slit S$$_2$$. The thickness of the sheets are different in different cases. The phase difference between the light waves reaching a point P on the screen from the two slits is denoted by $$\delta$$(P) and the intensity by I(P). Match each situation given in Column I with the statement(s) in Column II valid for that situation:
| Column I | Column II | ||
|---|---|---|---|
| (A) |  |
(P) | $$\delta ({P_0}) = 0$$ |
| (B) | $$(\mu-1)t=\lambda/4$$ |
(Q) | $$\delta ({P_1}) = 0$$ |
| (C) | $$(\mu-1)t=\lambda/2$$ |
(R) | $$I({P_1}) = 0$$ |
| (D) | $$(\mu-1)t=3\lambda/4$$ |
(S) | $$I({P_0}) > I({P_1})$$ |
| (T) | $$I({P_2}) > I({P_1})$$ |
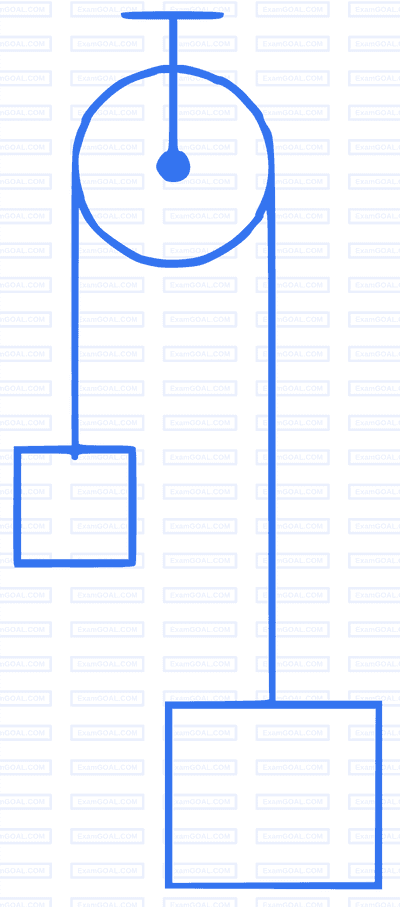
A light inextensible string that goes over a smooth fixed pulley as shown in the figure connects two blocks of masses 0.36 kg and 0.72 kg. Taking g = 10 m/s2, find the work done (in joules) by the string on the block of mass 0.36 kg during the first second after the system is released from rest.
Two soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8 N/m$$^2$$. The radii of bubbles A and B are 2 cm and 4 cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04 N/m. Find the ratio $$n_B/n_A$$, where $$n_A$$ and $$n_B$$ are the number of moles of air in bubbles A and B, respectively. (Neglect the effect of gravity.)