The IUPAC names of $$\mathbf{A}$$ and $$\mathbf{B}$$ are

The edge length of unit cell of a metal having molecular weight $$75 \mathrm{~g} \mathrm{~mol}^{-1}$$ is 5 $$\mathop A\limits^o $$ which crystallizes in cubic lattice. If the density is $$2 \mathrm{~g} / \mathrm{cc}$$, find the radius of metal atom. $$\left(\mathrm{N}_{\mathrm{A}}=6 \times 10^{23}\right)$$. Give the answer in $$\mathrm{pm}$$.

$$ \mathrm{B}(\mathrm{OH})_3+\mathrm{NaOH} \quad \mathrm{NaBO}_2+\mathrm{Na}\left[\mathrm{~B}(\mathrm{OH})_4\right] $$$+\mathrm{H}_2 \mathrm{O}$

How can this reaction be made to proceed in forward direction?

A solution when diluted with $\mathrm{H}_2 \mathrm{O}$ and boiled, it gives a white precipitate. On addition of excess $\mathrm{NH}_4 \mathrm{Cl} / \mathrm{NH}_4 \mathrm{OH}$, the volume of precipitate decreases leaving behind a white gelatinous precipitate. Identify the precipitate which dissolves in $\mathrm{NH}_4 \mathrm{OH} / \mathrm{NH}_4 \mathrm{Cl}$.

When benzene sulphonic acid and $p$-nitrophenol are treated with $\mathrm{NaHCO}_3$, the gases released respectively are

A monatomic ideal gas undergoes a process in which the ratio of P to V at any instant is constant and equals to 1 . What is the molar heat capacity of the gas?

(I) 1,2-Dihydroxybenzene

(II) 1,3-Dihydroxybenzene

(III) 1,4-Dihydroxybenzene

(IV) Hydroxy benzene

The increasing order of boiling points of the above mentioned alcohols is

$$ \begin{aligned} &\mathrm{CH}_3-\mathrm{CH}=\mathrm{CH}_2+\mathrm{NOCl} \rightarrow \mathrm{P}\\ &\text { Identify the adduct. } \end{aligned} $$

The IUPAC name of $\mathrm{C}_6 \mathrm{H}_5 \mathrm{COCl}$ is

$$ \begin{aligned} & \mathrm{Ag}^{+}+\mathrm{NH}_3 \quad\left[\mathrm{Ag}\left(\mathrm{NH}_3\right)\right]^{+} \\ & k_1=3.5 \times 10^{-3} \\ & {\left[\mathrm{Ag}\left(\mathrm{NH}_3\right]^{+}+\mathrm{NH}_3 \quad\left[\mathrm{Ag}\left(\mathrm{NH}_3\right)_2\right]^{+}\right.} \end{aligned} $$

$k_2=1.7 \times 10^{-3}$, then the formation constant of $\left[\mathrm{Ag}\left(\mathrm{NH}_3\right)_2\right]^{+}$ is :

$\mathrm{CH}_3 \mathrm{NH}_2+\mathrm{CHCl}_3+\mathrm{KOH} \rightarrow$ Nitrogen containing compound $+\mathrm{KCl}+\mathrm{H}_2 \mathrm{O}$.

Nitrogen containing compound is :

$\mathrm{CuSO}_4$ decolourises on addition of KCN , the product is

The direct conversion of A to B is difficult; hence, it is carried out by the following shown path:Given,

$$ \begin{aligned} & \Delta \mathrm{S}_{(\mathrm{A} \rightarrow \mathrm{C})}=50 \text { e.u. } \\ & \Delta \mathrm{S}_{(\mathrm{C} \rightarrow \mathrm{D})}=30 \text { e.u. } \\ & \Delta \mathrm{S}_{(\mathrm{B} \rightarrow \mathrm{D})}=20 \text { e.u. } \end{aligned} $$

Where e.u. is entropy unit. Then $\Delta \mathrm{S}_{(\mathrm{A} \rightarrow \mathrm{B})}$ is :

$$ \mathrm{N}_2+3 \mathrm{H}_2 \to 2 \mathrm{NH}_3 $$

Which is the correct statement if $\mathrm{N}_2$ is added at equilibrium condition?

If the bond length of CO bond in carbon monoxide is $1.128 \mathop {\rm{A}}\limits^{\rm{o}}$, then what is the value of CO bond length in $\mathrm{Fe}(\mathrm{CO})_5$?

Which of the following reactants on reaction with conc. NaOH followed by acidification gives the following lactone as the only product?

$$ \text { The major products } \mathbf{P} \text { and } \mathbf{Q} \text { are } $$

The given graph represents the variation of Z (compressibility factor $=\mathrm{PV} / n \mathrm{RT}$ ) versus P , for three real gases $\mathrm{A}, \mathrm{B}$ and C . Identify the only incorrect statement.

What are N and M?

How can the conversion of (i) to (ii) be brought about?

Which is the rate determining step in Hofmann bromamide degradation?

What are the constituent amines formed when the mixture of (i) and (ii) undergoes Hofmann bromamide degradation?

Predict the magnetic nature of $\mathbf{A}$ and $\mathbf{B}$.

The hybridisation of $A$ and $B$ are :

Which of the following option is correct?

What should be the age of fossil for meaningful determination of its age?

A nuclear explosion has taken place leading to increase in concentration of ${ }^{14} \mathrm{C}$ in nearby areas. ${ }^{14} \mathrm{C}$ concentration is $\mathrm{C}_1$ in nearby areas and $C_2$ in areas far away. If the age of the fossil is determined to be $T_1$ and $T_2$ at the places respectively then,

$$ \begin{array}{r} 2 \mathrm{Ag}^{+}+\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6+\mathrm{H}_2 \mathrm{O} \rightarrow 2 \mathrm{Ag}(\mathrm{~s})+\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_7 +2 \mathrm{H}^{+} \end{array} $$

Find $\ln \mathrm{K}$ of this reaction.

When ammonia is added to the solution, pH is raised to 11 . Which half-cell reaction is affected by pH and by how much?

Ammonia is always added in this reaction. Which of the following must be incorrect?

For the reaction, $2 \mathrm{CO}+\mathrm{O}_2 \rightarrow 2 \mathrm{CO}_2 ; \Delta \mathrm{H}=-560 \mathrm{~kJ}$. Two moles of CO and one mole of $\mathrm{O}_2$ are taken in a container of volume 1 L . They completely form two moles of $\mathrm{CO}_2$, the gases deviate appreciably from ideal behaviour. If the pressure in the vessel changes from 70 to 40 atm , find the magnitude (absolute value) of $\Delta \mathrm{U}$ at 500 K . $(1 \mathrm{~L} \mathrm{~atm}=0.1 \mathrm{~kJ})$

Match the extraction processes listed in Column I with metals listed in Column II.

$$ \text { Match the Column I with Column II : } $$

$$ \text { Match Column I with Column II : } $$

If $$w=\alpha+\mathrm{i} \beta$$, where $$\beta \neq 0$$ and $$z \neq 1$$, satisfies the condition that $$\left(\frac{w-\bar{w} z}{1-z}\right)$$ is purely real, then the set of values of $$z$$ is:

Let $$a, b, c$$ be the sides of a triangle. No two of them are equal and $$\lambda \in R$$. If the roots of the equation $$x^{2}+2(a+b+c) x+3 \lambda(a b+b c+c a)=0$$ are real, then,

If $$f''(x)=-f(x)$$ and $$g(x)=f'(x)$$ and $$\mathrm{F}(x)=\left(f\left(\frac{x}{2}\right)\right)^{2}+\left(g\left(\frac{x}{2}\right)\right)^{2}$$ and given that $$\mathrm{F}(5)=5$$, then $$\mathrm{F}(10)$$ is equal to :

Let $$\theta \in\left(0, \frac{\pi}{4}\right)$$ and $$t_{1}=(\tan \theta)^{\tan \theta}, t_{2}=(\tan \theta)^{\cot \theta}, t_{3}=(\cot \theta)^{\tan \theta}$$ and $$t_{4}=(\cot \theta)^{\cot \theta}$$, then

If $$\mathrm{P}\left(u_{i}\right) \propto i$$, where $$i=1,2,3, \ldots n$$, then $$\lim_\limits{n \rightarrow \infty} \mathrm{P}(w)$$ is equal to:

If $$\mathrm{P}\left(u_{i}\right)=c$$, where $$c$$ is a constant then $$\mathrm{P}\left(u_{n} / w\right)$$ is equal to:

If $$n$$ is even and E denotes the event of choosing even numbered urn $$\left(\mathrm{P}\left(u_{i}\right)=\frac{1}{n}\right)$$, then the value of $$\mathrm{P}(w / \mathrm{E})$$ is :

$$\int_\limits{0}^{\pi / 2} \sin x d x$$ is equal to:

If $$\lim_\limits{t \rightarrow a} \frac{\int_{a}^{t} f(x) d x-\frac{(t-a)}{2}\{f(t)+f(a)\}}{(t-a)^{3}}=0$$ then the degree of polynomial function $$f(x)$$ almost is:

$$f''(x) < 0 \forall x \in(a, b)$$ and $$c$$ is a point such that $$a < c < b$$, and $$(c, f(C))$$ is the point lying on the curve for which $$\mathrm{F}(C)$$ is maximum, then $$f'(C)$$ is equal to:

If $$f(x)$$ is a twice differentiable function such that $$f(A)=0, f(B)=2, f(C)=-1, f(D)=2$$, $$f(e)=0$$, where $$a < b < c < d < e$$, then the minimum number of zeroes of $$g(x)=\left(f'(x)\right)^{2}+f''(x) f(x)$$ in the interval $$[a, e]$$ is :

Match the following:

For $x>0, \mathop {\lim }\limits_{x \to 0}\left((\sin x)^{1 / x}+(1 / x)^{\sin x}\right)$ is :

$\int \frac{x^2-1}{x^3 \sqrt{2 x^4-2 x^2+1}} d x$ is equal to

Given an isosceles triangle, whose one angle is $120^{\circ}$ and radius of its incircle $=\sqrt{3}$. Then the area of the triangle in sq. units is

If $0<\theta<2 \pi$, then the intervals of values of $\theta$ for which $2 \sin ^2 \theta-5 \sin \theta+2>0$, is

A plane passes through $(1,-2,1)$ and is perpendicular to two planes $2 x-2 y+z=0$ and $x-y+2 z=4$. The distance of the plane from the point $(1,2,2)$ is:

If $f(x)=\min \left\{1, x^2, x^3\right\}$, then

A tangent drawn to the curve $y=f(x)$ at $\mathrm{P}(x, y)$ cuts the X -axis and Y -axis at A and B respectively such that $\mathrm{BP}: \mathrm{AP}=3: 1$, given that $f(1)=1$, then

If a hyperbola passes through the focus of the ellipse $\frac{x^2}{25}+\frac{y^2}{16}=1$ and its transverse and conjugate axes coincide with the major and minor axes of the ellipse, and the product of eccentricities is 1 , then

Internal bisector of $\angle A$ of triangle $A B C$ meets side BC at D . A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F . If $a, b, c$ represent sides of $\triangle \mathrm{ABC}$ then

$f(x)$ is cubic polynomial which has local maximum at $x=-1$. If $f(2)=18, f(1)=-1$ and $f(x)$ has local minima at $x=0$, then

$$ \begin{aligned} & f(x)=\left\{\begin{array}{cc} e^x, & 0 \leq x \leq 1 \\ 2-e^{x-1}, & 1 < x \leq 2 \\ x-e, & 2 < x \leq 3 \end{array} \quad\right. \text { and } \\ & g(x)=\int_0^x f(t) d t, x \in[1,3] \text { then } g(x) \text { has } \end{aligned} $$

If $P$ is a point on $C_1$ and $Q$ in another point on $\mathrm{C}_2$, then $\frac{\mathrm{PA}^2+\mathrm{PB}^2+\mathrm{PC}^2+\mathrm{PD}^2}{\mathrm{QA}^2+\mathrm{QB}^2+\mathrm{QC}^2+\mathrm{QD}^2}$ is equal to :

A circle touches the line $L$ and the circle $C_1$ externally such that both the circles are on the same side of the line, then the locus of center of the circle is:

A line $M$ through $A$ is drawn parallel to $B D$. Point $S$ moves such that its distances from

the line BD and the vertex A are equal. If locus of S cuts M at $\mathrm{T}_2$ and $\mathrm{T}_3$ and AC at $\mathrm{T}_1$, then area of $\Delta T_1 T_2 T_3$ is :

The sum of the elements of $\mathrm{U}^{-1}$ is:

The value of $\left[\begin{array}{lll}3 & 2 & 0\end{array}\right] U\left[\begin{array}{l}3 \\ 2 \\ 0\end{array}\right]$ is :

If roots of the equation $x^2-10 c x-11 d=0$ are $a, b$ and those of $x^2-10 a x-11 b=0$ are $c, d$, then the value of $a+b+c+d$ is $(a, b, c$ and $d$ are distinct numbers)

$$ \text { The value of } 5050 \frac{\int_0^1\left(1-x^{50}\right)^{100} d x}{\int_0^{\frac{1}{1}}\left(1-x^{50}\right)^{101} d x} \text { is : } $$

If $a_n=\frac{3}{4}-\left(\frac{3}{4}\right)^2+\left(\frac{3}{4}\right)^3+\cdots \cdots(-1)^{n-1}\left(\frac{3}{4}\right)^n$ and $b_n=1-a_n$, then find the minimum natural number $n_0$ such that $b_n>a_n \forall n>n_0$

If $f(x)$ is a twice differentiable function such that $f(A)=0, f(B)=2, f(C)=-1, f(D)=2$, $f(e)=0$, where $a < b < c < d < e$, then the minimum number of zeroes of $g(x)=\left(f^{\prime}(x)\right)^2 +f^{\prime \prime}(x) f(x)$ in the interval $[a, e]$ is :

$$ \text { Normals are drawn at points } \mathrm{P}, \mathrm{Q} \text { and } \mathrm{R} \text { lying on the parabola } y^2=4 x \text { which intersect at }(3,0) \text {. Then } $$

$$ \text { Match the following : } $$

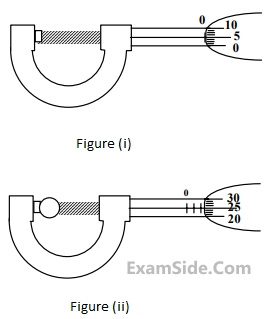
In a screw gauge, the zero of main scale coincides with the fifth division of circular scale in figure (i).The circular division of screw gauge is 50. It moves 0.5 mm on main scale in one rotation.The diameter of the ball in figure (ii) is

Match the following columns.

A solid sphere of radius $R$ has moment of inertia $I$ about its geometrical axis. If it is melted into a disc of radius $r$ and thickness $t$. If its moment of inertia about the tangential axis (which is perpendicular to plane of the disc), is also equal to $I$, then the value of $r$ is equal to

In the following circuits, it is given that $\mathrm{R}_1=1 \Omega, \mathrm{R}_2=2 \Omega, \mathrm{C}_1=2 \mu \mathrm{~F}$ and $\mathrm{C}_2=4 \mu \mathrm{~F}$.

Two blocks A and B of masses $2 m$ and $m$, respectively, are connected by a massless and inextensible string. The whole system is suspended by a massless spring as shown in the figure. The magnitudes of acceleration of A and B, immediately after the string is cut, are respectively,

A point object is placed at a distance of 20 cm from a thin plano-convex lens of focal length 15 cm , if the plane surface is silvered. The image will form at

A biconvex lens of focal length $f$ forms a circular image of sun of radius $r$ in focal plane. Then

Graph of position of image versus position of point object from a convex lens is shown. Then, the focal length of the lens is

A massless rod is suspended by two identical strings AB and CD of equal length. A block of mass $m$ is suspended from point $O$ such that BO is equal to $x$. Further, it is observed that the frequency of 1st harmonic (fundamental frequency) in AB is equal to 2 nd harmonic frequency in CD. Then, length of BO is

A system of binary stars of masses $m_{\mathrm{A}}$ and $m_{\mathrm{B}}$ are moving in circular orbits of radii $r_{\mathrm{A}}$ and $r_R$, respectively. If $\mathrm{T}_A$ and $\mathrm{T}_B$ are the time periods of masses $m_A$ and $m_B$ respectively, then

Consider a cylindrical element as shown in the figure. The current that flows through the element is I and resistivity of material of the cylinder is $\rho$. Choose the correct option out the following

In the given diagram, a line of force of a particular force field is shown. Out of the following options, it can never represent

The electrostatic potential $\left(\phi_r\right)$ of a spherical symmetric system, kept at origin, is shown in the adjacent figure, and given as

$$ \begin{array}{ll} \phi_r=\frac{q}{4 \pi \epsilon_0 r} & \left(r \geq \mathrm{R}_0\right) \\ \phi_r=\frac{q}{4 \pi \epsilon_0 \mathrm{R}_0} & \left(r \leq \mathrm{R}_0\right) \end{array} $$

A solid cylinder of mass m and radius $r$ is rolling on rough inclined plane of inclination $\theta$. The coefficient of friction between the cylinder and incline is $\mu$. then

Function $x=\mathrm{A} \sin ^2 \omega t+\mathrm{B} \cos ^2 \omega t+\mathrm{C} \sin \omega t \cos \omega t$ represents SHM

In a dark room with ambient temperature $\mathrm{T}_0$, a black body is kept at a temperature T . Keeping the temperature of the black body constant (at T), sunrays are allowed to fall on the black body through a hole in the roof of the dark room. Assuming that there is no change in the ambient temperature of the room, which of the following statement(s) is/are correct?

The graph between $\frac{1}{\lambda}$ and stopping potential (V) of three metals having work functions $\phi_1, \phi_2$, and $\phi_3$ in an experiment of photoelectric effect is plotted as shown in the figure. Which of the following statement(s) is/are correct? (Here, $\lambda$ is the wavelength of the incident ray).

An infinite current-carrying wire passes through point O and in perpendicular to the plane containing a current-carrying loop ABCD as shown in the figure. Choose the correct option(s):

A ball moves over a fixed track as shown in the figure. From $A$ to $B$, the ball rolls without slipping. Surface $B C$ is frictionless. $K_A, K_B$ and $K_c$ are kinetic energies of the ball at $A, B$ and C , respectively. Then

Initially, the capacitor was uncharged. Now, switch $S_1$ is closed and $S_2$ is kept open. If time constant of this circuit is $\tau$, then

After the capacitor gets fully charged, $\mathrm{S}_1$ is opened and $S_2$ is closed so that the inductor is connected in series with the capacitor. Then,

If the total charge stored in the LC circuit.is $\mathrm{Q}_0$, then for $t \geq 0$,

If the level of liquid starts decreasing slowly when the level of liquid is at a height $h_1$ above the cylinder, the block just starts moving up. Then, the value of $h_1$ is:

Let the cylinder is prevented from moving up, by applying a force and water level is further decreased. Then, the height of water level ( $h_2$ in the figure) for which the cylinder remains in original position without application of force is

If the height $h_2$ of water level is further decreased, then

Find the number of times the intensity is maximum in the time interval of 1 sec.

Find the wave velocity of louder sound.

Find the number of times $y_1+y_2=0$ at $x=0$ in $1 s$.

What is the advantage of this system?

What is the disadvantage of this system?

Which force causes the train to elevate upwards

There is a rectangular plate of mass M kg of dimensions ( $a \times b$ ). The plate is held in horizontal position by striking $n$ small balls each of mass m per unit area per unit time. These are striking in the shaded half region of the plate. The balls are colliding elastically with velocity $v$. What is $v$ ?

In an insulated vessel, 0.05 kg steam at 373 K and 0.45 kg of ice at 253 K are mixed. Then, find the final temperature of the mixture.

In hydrogen-like atom $(z=11)$, $n$th line of Lyman series has wavelength A equal to the de Broglie's wavelength of electron in the level from which it originated. What is the value of $n$ ?

A circular disc with a groove along its diameter is placed horizontally. A block of mass 1 kg is placed as shown. The coefficient of friction between the block and all surfaces of groove in contact is $\mu=\frac{2}{5}$. The disc has an acceleration of $25 \mathrm{~m} / \mathrm{s}^2$. Find the acceleration of the block with respect to disc.

Heat given to the processes is positive. Match Column I with Column II:

$$ \text { Match the following Columns. } $$

$$ \text { Match the following Columns. } $$

A simple telescope used to view distant objects has eyepiece and objective lens of focal lengths $f_e$ and $f_0$, respectively. Match Column I with Column II: