IIT-JEE 1998
Paper was held on
Sat, Apr 11, 1998 9:00 AM
Chemistry
1
An aqueous solution containing 0.10 g KIO3 (formula weight = 214.0) was treated with an excess of KI solution. The solution was acidified with HCl. The liberated I2 consumed 45.0 mL of thiosulphate solution to decolourise the blue strach-iodine complex. Calculate the molarity of the sodium thiosulphate solution.
2
The orbital diagram in which the Aufbau principle is violated is
3
Interpret the non-linear shape of H2S molecule and non-planar shape of PCl3 using valence shell electron pair repulsion (VSEPR) theory. (Atomic numbers : H = 1, P = 15, S = 16, Cl = 17)
4
The rate constant of a reaction is 1.5 $$\times$$ 107 s-1 at 50oC and 4.5 $$\times$$ 107 s-1 at 100oC. Evaluate the Arrhenius parameters A and Ea.
5
Find the solubility product of a saturated solution of Ag2CrO4 in water at 298 K if the emf of the cell Ag|Ag+ (satd. Ag2CrO4 soln.) || Ag+ (0.1 M) | Ag is 0.164 V at 298 K.
6
Calculate the equilibrium constant for the reaction:
2Fe3+ + 3I- $$\leftrightharpoons$$ 2Fe2+ + $$I_3^-$$. The standard reduction potentials in acidic conditions are 0.78 V and 0.54 V respectively for Fe3+ | Fe2+ and $$I_3^-$$ | I- couples.
2Fe3+ + 3I- $$\leftrightharpoons$$ 2Fe2+ + $$I_3^-$$. The standard reduction potentials in acidic conditions are 0.78 V and 0.54 V respectively for Fe3+ | Fe2+ and $$I_3^-$$ | I- couples.
7
A solution of a nonvolatile solute in water freezes at -0.30oC. The vapour pressure of pure water at 298 K s 23.51 mm Hg and Kf for water is 1.86 K kg mol-1. Calculate the vapour pressure of this solution at 298 K.
8
Hydrogen peroxide acts both as an oxidising and as a reducing agent in alkaline solution towards certain first row transition metal ions. Illustrate both these properties of H2O2 using chemical equations.
9
Work out the following using chemical equation :
Chlorination of calcium hydroxide produces bleaching powder.
Chlorination of calcium hydroxide produces bleaching powder.
10
Highly pure dilute solution of sodium in liquid ammonia
11
Read the following Assertion and Reason and answer as per the options given below
Assetion: LiCl is predominantly a covalent compound
Reason : Electronegativity difference between Li and Cl is too small
Assetion: LiCl is predominantly a covalent compound
Reason : Electronegativity difference between Li and Cl is too small
12
The geometry and the type of hybrid orbital present about the central atom in BF3 is
13
ASSERTION:
Nuclide $${}_{13}^{30}Al$$ is less stable than $${}_{20}^{40}Ca$$
REASON:
Nuclides having odd number of protons and neutrons are generally unstable.
Nuclide $${}_{13}^{30}Al$$ is less stable than $${}_{20}^{40}Ca$$
REASON:
Nuclides having odd number of protons and neutrons are generally unstable.
14
Which of the following statement(s) is (are) correct?
15
Decrease in atomic number is observed during
16
The energy of an electron in the first Bohr orbit of H atom is -13.6 eV. The possible energy value(s) of the excited state(s) for electrons in Bohr orbits of hydrogen is (are)
Mathematics
1
A fair coin is tossed repeatedly. If the tail appears on first four tosses, then the probability of the head appearing on the fifth toss equals
2
For any two vectors $$u$$ and $$v,$$ prove that
(a) $${\left( {u\,.\,v} \right)^2} + {\left| {u \times v} \right|^2} = {\left| u \right|^2}{\left| v \right|^2}$$ and
(b) $$\left( {1 + {{\left| u \right|}^2}} \right)\left( {1 + {{\left| v \right|}^2}} \right) = {\left( {1 - u.v} \right)^2} + {\left| {u + v + \left( {u \times v} \right)} \right|^2}.$$
(a) $${\left( {u\,.\,v} \right)^2} + {\left| {u \times v} \right|^2} = {\left| u \right|^2}{\left| v \right|^2}$$ and
(b) $$\left( {1 + {{\left| u \right|}^2}} \right)\left( {1 + {{\left| v \right|}^2}} \right) = {\left( {1 - u.v} \right)^2} + {\left| {u + v + \left( {u \times v} \right)} \right|^2}.$$
3
Prove, by vector methods or otherwise, that the point of intersection of the diagonals of a trapezium lies on the line passing through the mid-points of the parallel sides. (You may assume that the trapezium is not a parallelogram.)
4
Which of the following expressions are meaningful?
5
For three vectors $$u,v,w$$ which of the following expression is not equal to any of the remaining three?
6
If $$a = i + j + k,\overrightarrow b = 4i + 3j + 4k$$ and $$c = i + \alpha j + \beta k$$ are linearly dependent vectors and $$\left| c \right| = \sqrt 3 ,$$ then
7
Let $${C_1}$$ and $${C_2}$$ be the graphs of the functions $$y = {x^2}$$ and $$y = 2x,$$ $$0 \le x \le 1$$ respectively. Let $${C_3}$$ be the graph of a function $$y=f(x),$$ $$0 \le x \le 1,$$ $$f(0)=0.$$ For a point $$P$$ on $${C_1},$$ let the lines through $$P,$$ parallel to the axes, meet $${C_2}$$ and $${C_3}$$ at $$Q$$ and $$R$$ respectively (see figure.) If for every position of $$P$$ (on $${C_1}$$ ), the areas of the shaded regions $$OPQ$$ and $$ORP$$ are equal, determine the function$$f(x).$$
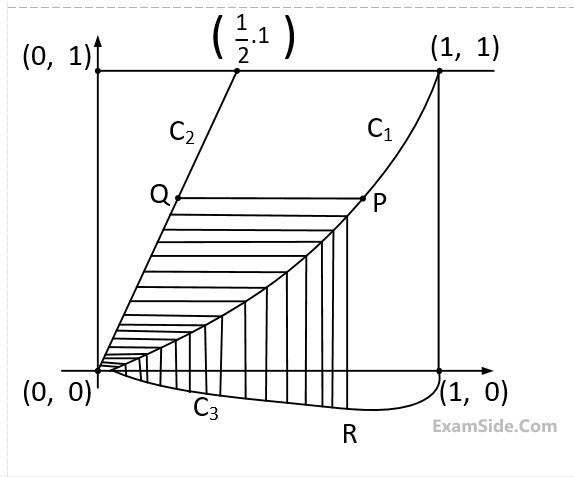

8
Three players, $$A,B$$ and $$C,$$ toss a coin cyclically in that order (that is $$A, B, C, A, B, C, A, B,...$$) till a head shows. Let $$p$$ be the probability that the coin shows a head. Let $$\alpha ,\,\,\,\beta $$ and $$\gamma $$ be, respectively, the probabilities that $$A, B$$ and $$C$$ gets the first head. Prove that $$\beta = \left( {1 - p} \right)\alpha $$ Determine $$\alpha ,\beta $$ and $$\gamma $$ (in terms of $$p$$).
9
Seven white balls and three black balls are randomly placed in a row. The probability that no two black balls are placed adjacently equals
10
There are four machines and it is known that exactly two of them are faulty. They are tested, one by one, in a random order till both the faulty machines are identified. Then the probability that only two tests are needed is
11
If $$E$$ and $$F$$ are events with $$P\left( E \right) \le P\left( F \right)$$ and $$P\left( {E \cap F} \right) > 0,$$ then
12
If $$\overline E $$ and $$\overline F $$ are the complementary events of events $$E$$ and $$F$$ respectively and if $$0 < P\left( F \right) < 1,$$ then
13
If from each of the three boxes containing $$3$$ white and $$1$$ black, $$2$$ white and $$2$$ black, $$1$$ white and $$3$$ black balls, one ball is drawn at random, then the probability that $$2$$ white and $$1$$ black ball will be drawn is
14
The order of the differential equation whose general solution is given by
$$y = \left( {{C_1} + {C_2}} \right)\cos \left( {x + {C_3}} \right) - {C_4}{e^{x + {C_5}}},$$ where
$${C_1},{C_2},{C_3},{C_4},{C_5},$$ are arbitrary constants, is
$$y = \left( {{C_1} + {C_2}} \right)\cos \left( {x + {C_3}} \right) - {C_4}{e^{x + {C_5}}},$$ where
$${C_1},{C_2},{C_3},{C_4},{C_5},$$ are arbitrary constants, is
15
Prove that $$\int_0^1 {{{\tan }^{ - 1}}} \,\left( {{1 \over {1 - x + {x^2}}}} \right)dx = 2\int_0^1 {{{\tan }^{ - 1}}} \,x\,dx.$$
Hence or otherwise, evaluate the integral
$$\int_0^1 {{{\tan }^{ - 1}}\left( {1 - x + {x^2}} \right)dx.} $$
Hence or otherwise, evaluate the integral
$$\int_0^1 {{{\tan }^{ - 1}}\left( {1 - x + {x^2}} \right)dx.} $$
16
Let $$f\left( x \right) = x - \left[ x \right],$$ for every real number $$x$$, where $$\left[ x \right]$$ is the integral part of $$x$$. Then $$\int_{ - 1}^1 {f\left( x \right)\,dx} $$ is
17
An n-digit number is a positive number with exactly digits. Nine hundred distinct n-digit numbers are to be formed using only the three digits 2, 5 and 7. The smallest value of n for which this is possible is
18
Using co-ordinate geometry, prove that the three altitudes of any triangle are concurrent.
19
If the vertices $$P, Q, R$$ of a triangle $$PQR$$ are rational points, which of the following points of the triangle $$PQR$$ is (are) always rational point(s)?
20
If $$\left( {P\left( {1,2} \right),\,Q\left( {4,6} \right),\,R\left( {5,7} \right)} \right)$$ and $$S\left( {a,b} \right)$$ are the vertices of a parrallelogram $$PQRS,$$ then
21
The diagonals of a parralleogram $$PQRS$$ are along the lines $$x + 3y = 4$$ and $$6x - 2y = 7$$. Then $$PQRS$$ must be a.
22
If $$x > 1,y > 1,z > 1$$ are in G.P., then $${1 \over {1 + In\,x}},{1 \over {1 + In\,y}},{1 \over {1 + In\,z}}$$ are in
23
Let $${T_r}$$ be the $${r^{th}}$$ term of an A.P., for $$r=1, 2, 3, ....$$ If for some positive integers $$m$$, $$n$$ we have
$${T_m} = {1 \over n}$$ and $${T_n} = {1 \over m},$$ then $${T_n} = {1 \over m},$$ equals
$${T_m} = {1 \over n}$$ and $${T_n} = {1 \over m},$$ then $${T_n} = {1 \over m},$$ equals
24
Let $$n$$ be an odd integer. If $$\sin n\theta = \sum\limits_{r = 0}^n {{b_r}{{\sin }^r}\theta ,} $$ for every value of $$\theta ,$$ then
25
Let $$p$$ be a prime and $$m$$ a positive integer. By mathematical induction on $$m$$, or otherwise, prove that whenever $$r$$ is an integer such that $$p$$ does not divide $$r$$, $$p$$ divides $${}^{np}{C_r},$$
[Hint: You may use the fact that $${\left( {1 + x} \right)^{\left( {m + 1} \right)p}} = {\left( {1 + x} \right)^p}{\left( {1 + x} \right)^{mp}}$$]
26
If the circle $${x^2}\, + \,{y^2} = \,{a^2}$$ intersects the hyperbola $$xy = {c^2}$$ in four points $$P\,({x_1},\,{y_1}),\,Q\,\,({x_2},\,{y_2}),\,\,R\,({x_3},\,{y_3}),\,S\,({x_4},\,{y_4}),$$ then
27
If $${a_n} = \sum\limits_{r = 0}^n {{1 \over {{}^n{C_r}}},\,\,\,then\,\,\,\sum\limits_{r = 0}^n {{r \over {{}^n{C_r}}}} } $$ equals
28
Number of divisor of the form 4$$n$$$$ + 2\left( {n \ge 0} \right)$$ of the integer 240 is
29
Prove that $$\tan \,\alpha + 2\tan 2\alpha + 4\tan 4\alpha + 8\cot 8\alpha = \cot \alpha $$
30
Which of the following number(s) is /are rational?
31
The number of values of $$x\,\,$$ in the interval $$\left[ {0,\,5\pi } \right]$$ satisfying the equation $$3\,{\sin ^2}x - 7\,\sin \,x + 2 = 0$$ is
32
If $$\,\left| {\matrix{
{6i} & { - 3i} & 1 \cr
4 & {3i} & { - 1} \cr
{20} & 3 & i \cr
} } \right| = x + iy$$ , then
33
The value of the sum $$\,\,\sum\limits_{n = 1}^{13} {({i^n}} + {i^{n + 1}})$$ , where i = $$\sqrt { - 1} $$, equals
34
Let $${A_0}{A_1}{A_2}{A_3}{A_4}{A_5}$$ be a regular hexagon inscribed in a circle of unit radius. Then the product of the lengths of the line segments $${A_0}{A_1},{A_0}{A_2}$$ and $${A_0}{A_4}$$ is
35
If $$\int_0^x {f\left( t \right)dt = x + \int_x^1 {t\,\,f\left( t \right)\,\,dt,} } $$ then the value of $$f(1)$$ is
36
Suppose $$f(x)$$ is a function satisfying the following conditions
(a) $$f(0)=2,f(1)=1$$,
(b) $$f$$has a minimum value at $$x=5/2$$, and
(c) for all $$x$$, $$$f'\left( x \right) = \matrix{ {2ax} & {2ax - 1} & {2ax + b + 1} \cr b & {b + 1} & { - 1} \cr {2\left( {ax + b} \right)} & {2ax + 2b + 1} & {2ax + b} \cr } $$$
where $$a,b$$ are some constants. Determine the constants $$a, b$$ and the function $$f(x)$$.
(a) $$f(0)=2,f(1)=1$$,
(b) $$f$$has a minimum value at $$x=5/2$$, and
(c) for all $$x$$, $$$f'\left( x \right) = \matrix{ {2ax} & {2ax - 1} & {2ax + b + 1} \cr b & {b + 1} & { - 1} \cr {2\left( {ax + b} \right)} & {2ax + 2b + 1} & {2ax + b} \cr } $$$
where $$a,b$$ are some constants. Determine the constants $$a, b$$ and the function $$f(x)$$.
37
A curve $$C$$ has the property that if the tangent drawn at any point $$P$$ on $$C$$ meets the co-ordinate axes at $$A$$ and $$B$$, then $$P$$ is the mid-point of $$AB$$. The curve passes through the point $$(1, 1)$$. Determine the equation of the curve.
38
Let $$h\left( x \right) = f\left( x \right) - {\left( {f\left( x \right)} \right)^2} + {\left( {f\left( x \right)} \right)^3}$$ for every real number $$x$$. Then
39
If $$f\left( x \right) = {{{x^2} - 1} \over {{x^2} + 1}},$$ for every real number $$x$$, then the minimum value of $$f$$
40
The number of values of $$x$$ where the function
$$f\left( x \right) = \cos x + \cos \left( {\sqrt 2 x} \right)$$ attains its maximum is
$$f\left( x \right) = \cos x + \cos \left( {\sqrt 2 x} \right)$$ attains its maximum is
41
Prove that a triangle $$ABC$$ is equilateral if and only if $$\tan A + \tan B + \tan C = 3\sqrt 3 $$.
42
A bird flies in a circle on a horizontal plane. An observer stands at a point on the ground. Suppose $${60^ \circ }$$ and $${30^ \circ }$$ are the maximum and the minimum angles of elevation of the bird and that they occur when the bird is at the points $$P$$ and $$Q$$ respectively on its path. Let $$\theta $$ be the angle of elevation of the bird when it is a point on the are of the circle exactly midway between $$P$$ and $$Q$$. Find the numerical value of $${\tan ^2}\theta $$. (Assume that the observer is not inside the vertical projection of the path of the bird.)
43
If $${\omega}$$ is an imaginary cube root of unity, then $${(1\, + \omega \, - {\omega ^2})^7}$$ equals
44
If in a triangle $$PQR$$, $$\sin P,\sin Q,\sin R$$ are in $$A.P.,$$ then
45
If$$\,\,\,$$ $$y = {{a{x^2}} \over {\left( {x - a} \right)\left( {x - b} \right)\left( {x - c} \right)}} + {{bx} \over {\left( {x - b} \right)\left( {x - c} \right)}} + {c \over {x - c}} + 1$$,
prove that $${{y'} \over y} = {1 \over x}\left( {{a \over {a - x}} + {b \over {b - x}} + {c \over {c - x}}} \right)$$.
prove that $${{y'} \over y} = {1 \over x}\left( {{a \over {a - x}} + {b \over {b - x}} + {c \over {c - x}}} \right)$$.
46
The angle between a pair of tangents drawn from a point $$P$$ to the parabola $${y^2} = 4ax$$ is $${45^ \circ }$$. Show that the locus of the point $$P$$ is a hyperbola.
47
If $$P=(x, y)$$, $${F_1} = \left( {3,0} \right),\,{F_2} = \left( { - 3,0} \right)$$ and $$16{x^2} + 25{y^2} = 400,$$ then $$P{F_1} + P{F_2}$$ equals
48
The number of values of $$c$$ such that the straight line $$y=4x + c$$ touches the curve $$\left( {{x^2}/4} \right) + {y^2} = 1$$ is
49
$$C_1$$ and $$C_2$$ are two concentric circles, the radius of $$C_2$$ being twice that of $$C_1$$. From a point P on $$C_2$$, tangents PA and PB are drawn to $$C_1$$. Prove that the centroid of the triangle PAB lies on $$C_1$$.
50
The number of common tangents to the circles $${x^2}\, + \,{y^2} = 4$$ and $${x^2}\, + \,{y^2}\, - 6x\, - 8y = 24$$ is