Let P be linearity, Q be time-invariance, R be causality and S be stability.

A discrete time system has the input-output relationship,

$$y\left( n \right) = \left\{ {\matrix{ {x\left( n \right),} & {n \ge 1} \cr {0,} & {n = 0} \cr {x\left( {n + 1} \right),} & {n \le - 1} \cr } } \right.$$

Where $$x\left( n \right)\,$$ is the input and $$y\left( n \right)\,$$ is the output. The above system has the properties

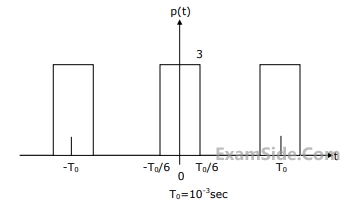
Let x(t) = $$\,2\cos (800\pi t) + \cos (1400\pi t)$$. x(t) is sampled with the rectangular pulse train shown in figure. The only spectral components (in KHz) present in the sampled signal in the frequency range 2.5 kHz to 3.5 kHz are

The system under consideration is an RC low -pass filter (RC-LPF) with R = 1.0 $$k\Omega $$ and C = 1.0 $$\mu F$$.

Let H(t) denote the frequency response of the RC-LPF. Let $${f_1}$$ be the highest frequency such that $$0 \le \left| f \right| \le {f_1},{{\left| {H({f_1})} \right|} \over {H(0)}} \ge 0.95$$. Then $${f_1}$$ (in Hz) is

The system under consideration is an RC low -pass filter (RC-LPF) with R = 1.0 $$k\Omega $$ and C = 1.0 $$\mu F$$.

Let $${t_g}$$ (f) be the group delay function of the given RC-LPF and $${f_2}$$ = 100 Hz. Then $${t_g}$$$${(f_2)}$$ in ms, is