The apparent wavelength of light from a star moving away from the earth is $0.02 \%$ more than the actual wavelength. The velocity of star is $\left[\mathrm{c}=\right.$ velocity of light $\left.=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right]$

In Young's double slit experiment with monochromatic light of wavelength 600 nm , the distance between the slits is $10^{-3} \mathrm{~m}$. For changing the fringe width by $3 \times 10^{-5} \mathrm{~m}$

a. the screen is moved away from the slit by 5 cm .

b. the screen is moved 5 cm towards the slits.

c. the screen is moved 3 cm towards the slits.

d. the screen is moved away from the slits by 3 cm .

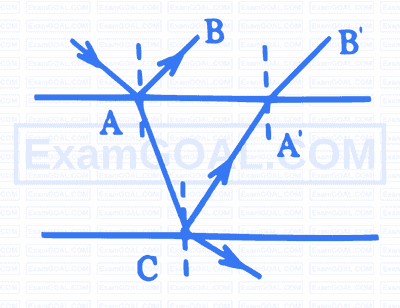
A ray of light of intensity ' I ' is incident on a parallel glass slab at a point ' $A$ ' as shown in figure. It undergoes partial reflection and refraction. At each reflection $25 \%$ of incident energy is reflected. The rays $A B$ and $A B$ undergo interference. The ratio $\frac{\mathrm{I}_{\text {max }}}{\mathrm{I}_{\text {min }}}$ is

In Young's double slit experiment, the distance between screen and aperture is 1 m . The slit width is 2 mm . Light of $6000 \mathop {\rm{A}}\limits^{\rm{o}}$ is used. If a thin glass plate ( $\mu=1.5$ ) of thickness 0.04 mm is placed over one of the slits, then there will be a lateral displacement of the fringes by