Four polaroids are placed such that the optic axis of each is inclined at an angle of $30^{\circ}$ the optic axis of the preceding one. If unpolarised light of intensity ' $\mathrm{I}_0$ ' falls on the first polaroid, the intensity of light transmitted from the fourth polaroid is $\left[\cos 30^{\circ}=\frac{\sqrt{3}}{2}\right]$

The apparent wavelength of light from a star moving away from the earth is $0.02 \%$ more than the actual wavelength. The velocity of star is $\left[\mathrm{c}=\right.$ velocity of light $\left.=3 \times 10^8 \mathrm{~m} / \mathrm{s}\right]$

In Young's double slit experiment with monochromatic light of wavelength 600 nm , the distance between the slits is $10^{-3} \mathrm{~m}$. For changing the fringe width by $3 \times 10^{-5} \mathrm{~m}$

a. the screen is moved away from the slit by 5 cm .

b. the screen is moved 5 cm towards the slits.

c. the screen is moved 3 cm towards the slits.

d. the screen is moved away from the slits by 3 cm .

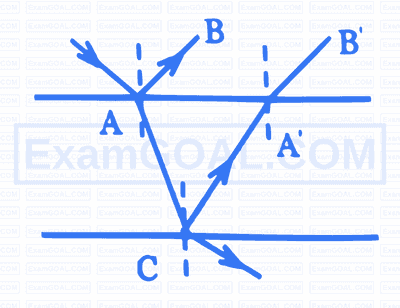
A ray of light of intensity ' I ' is incident on a parallel glass slab at a point ' $A$ ' as shown in figure. It undergoes partial reflection and refraction. At each reflection $25 \%$ of incident energy is reflected. The rays $A B$ and $A B$ undergo interference. The ratio $\frac{\mathrm{I}_{\text {max }}}{\mathrm{I}_{\text {min }}}$ is